f kwadratowa
Loyal: liczby −5 i 3 są miejscami zerowymi funkcji kwadratowej f, a punkt P (1,3) należy do jej
wykresu. Podaj wzór tej funkcji
16 lut 23:48
Radek:
f(x)=a(x−3)(x+5)
f(x)=a(1−3)(1+5)=3
16 lut 23:51
Eta:
z postaci iloczynowej: f(x)=a(x+5)(x−3) i P(1,3)
to: 3=a(1+5)(1−3) ⇒ a=....
f(x)=....
16 lut 23:51
Godzio:
Zawsze wszystkim, których uczę, przy funkcji kwadratowej, mówię jedną rzecz:
Masz w poleceniu "miejsca zerowe" PISZESZ OD RAZU POSTAĆ ILOCZYNOWĄ, a jeżeli masz "współrzędne
wierzchołka / zbiór wartości + oś symetrii / największa/najmniejsza wartość dla argumentu"
PISZESZ OD RAZU POSTAĆ KANONICZNĄ.
Tutaj mamy miejsca zerowe no to :
f(x) = a(x − x
1)(x − x
2)
x
1 = −5, x
2 = 3
f(x) = a(x + 5)(x + 3) do tego wiesz, że P(1,3) ⇒ x = 1, y = 3 należy do wykresu:
| | 1 | |
3 = a(1 + 5)(1 + 3) ⇒ a = |
| |
| | 8 | |
| | 1 | |
f(x) = |
| (x + 5)(x + 3) (można tak zostawić, bo nie pytają o postać ogólną) |
| | 8 | |
16 lut 23:52
Eta:
Ejjj
Godzio 
16 lut 23:54
Eta:
popraw

16 lut 23:55
Loyal: jak miejsca zerowe −5 i 3 i 1/8 czyli ramiona w górę? to nie idzie...
16 lut 23:55
Loyal: wczesniej obliczalem z postaci iloczynowej i mi wyszlo a= −1/4 ale usilnie próbowałem
przekształcić do postaci ogólnej mając w treści: Podaj wzór funkcji f...
16 lut 23:58
Godzio:
Pospieszyłem się

f(x) = a(x + 5)(x − 3)
Dalej analogicznie (liczy się tylko początek)

16 lut 23:58
Godzio:
Loyal a czemu nie ? (abstrahując od tego, że się pomyliłem)
| | 1 | |
f(x) = |
| (x + 5)(x − 3) − taka funkcja też istnieje  |
| | 8 | |
17 lut 00:00
Loyal: Z twojego zapisu wynika, że pierwiastki to: −5, 3 a więc p=xw= −1
Wykres przechodzi przez punkt P(1,3), ramiona paraboli są w górę, więc siłą rzeczy, nie przejdą
przez punkt (3,0) i jednocześnie przez (1,3)
17 lut 00:04
Godzio: No wiadomo, jak dodamy ten warunek, że przechodzi przez punkt, to zgoda, ale bez niego, czemu
nie

17 lut 00:06
Loyal: Nie sprecyzowałem, oczywiście cały czas nawiązywałem do tego zadania
17 lut 00:07
Godzio:
No to już wszystko wiemy

17 lut 00:08
Eta:
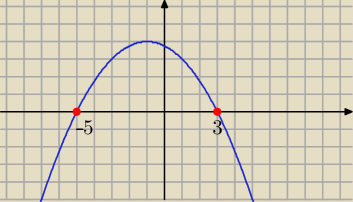
17 lut 00:11


 f(x) = a(x + 5)(x − 3)
Dalej analogicznie (liczy się tylko początek)
f(x) = a(x + 5)(x − 3)
Dalej analogicznie (liczy się tylko początek) 



