Pochodne, całki, studia Piotr: Błagam o pomoc: W środę mam II termin sesji: Wyznaczyć przedziały monotoniczności oraz ekstrema lokalne funkcji: f(x) = (x³) / (x+1)² oraz dla drugiej funkcji f(x)= (x³)/(x−1)² Siedzę od kilku dni i wychodzą jakieś głupoty, w internecie jest tyle róznych pomocy że ja już zgłupiałem, nie wiem jak mam ja to liczyć. Wychodzą dziwne pochodne. I jeszcze obliczyć całkę na górze +nieskończoność a na dole 0 : 1 / (x+1)³ dx => mi wychodzi −1

kaka: To przedstaw swojeo bliczenia!

kaka: https://matematykaszkolna.pl/strona/3420.html

kika: Ta wiedza była w programie LO.i technikach

Ajtek: kika dawno temu to było. Teraz przebiegu zmienności funkcji nie ma w szkole średniej. O całkach nie wspomnę.

kika: Tak , Ajtku, ale zainteresowany czeka na" gotowca"

Ajtek: Dlatego nie robię .

Mila:

	x3
f(x) =
	(x+1)2

1) D: x∊R\{−1} [ x+1≠0] 2) miejsca zerowe: x³=0⇔x=0 3) monotoniczność i ekstrema:

	3x2*(x+1)2−x3*2*(x+1)
f'(x)=		⇔
	(x+1)4

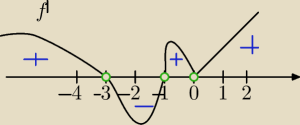
f'(x)=U{x²*(x+3)}{(x+1)³ f'(x)=0⇔x=0 lub x=−3 ewentualne ekstrema dla tych x−ów f'(x)>0⇔x∊(−∞,−3)U(−1,0)U(0,∞) f(x) rosnąca dla x∊(−∞,−3)U(−1,0)U(0,∞) dla x=−3 pochodna zmienia znak z dodatniej na ujemną⇔ dla x=−3 funkcja ma maksimum lokalne w x=−1 jest nieciągła w x=0 ma punkt przegięcia f(x) malejąca dla x∊(−3,−1)

Ajtek: Hej Mila . Masz za dobre

Mila:

	−27
ymaks=f(−3) =
	4

	x3
f(x)=
	(1+x)2

Mila: A student Ajtku na randce.?

Ajtek: Mila a jak myślisz Gotowca szukał. Niech myśli co, skąd i dlaczego. Na egzamie radosna twórczość. Mila naprawdę czasami mi szkoda Twojego czasu. Za dobra jesteś dla leni, moje to zdanie.

Mila: Prawda wypłynie jak oliwa na wodę. Pozdrawiam Cię Ajtku Dobranoc. Teraz bedzie lekturka.