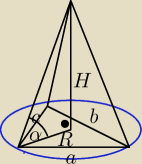
podstawą ostrosłupa jest trójkąt agusiakk95: Podstawą ostrosłupa jest trójkąt o bokach 3,7,8. Spodek wysokości ostrosłupa jest środkiem okręgu opisanego na podstawie a krawędź boczna jest nachylona do podstawy pod kątem 60 stopni. Wyznacz objętość ostrosłupa.

Alfa: w podstawie: a = 8, b = 7, c = 3 α = 60^o pole podstawy można policzyć ze wzoru Herona:

	a+b+c
p =		= 9
	2

P_p = √9*(9−8)(9−7)(9−3) = √9*1*2*6 = 6√3

	abc
z zależności: PΔ =		można obliczyć promień okręgu opisanego na podstawie:
	4R

	8*7*3
6√3 =
	4R

	42
R =
	6√3

	7√3
R =
	3

wysokość ostrosł. można obliczyć z funkcji tryg.:

	H
tg60o =
	R

. . . H = ... i na koniec objętość:

	1
V =		Pp*H = ...
	3

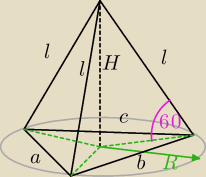dero2005: P_p = √p(p−a)(p−b)(p−c)

	a+b+c
gdzie p =
	2

	a*b*c
R =
	4Pp

H = R*tg60^o = R√3

	Pp*H
V =		=
	3