@
qu: Proszę o sprawdzenie
Oblicz długość krawędzi bocznej i długość krawędzi podstawy graniastosłupa prawidłowego
sześciokątnego, którego najdłuższa przekątna wynosi 3
√5 a pole pow bocznej 54
Wychodził mi kosmos
2 równania
dzielenie wielomianów itp
grupowanie
po zabiegach i odrzuceniu wartości ujemnych wyszło
2 możliwości

a=3 i h=3
albo
a= 3/2 i h=6
Jakby ktoś mógł to sprawdzić byłym wdzięczny

Bogdan:
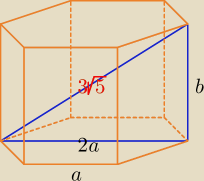
Można tak rozwiązać: a > 0, b > 0
| | 2 | |
6ab = 54 /* |
| ⇒ 4ab = 36 i 4a2 + b2 = 45 ⇒ 4a2 + 4ab + b2 = 45 + 4ab |
| | 3 | |
(2a + b)
2 = 45 + 36 ⇒ 2a + b = 9 ⇒ b = 9 − 2a lub 2a + b = −9 sprzeczność
6ab = 54 ⇒ ab = 9 ⇒ a(9 − 2a) = 9 ⇒ 2a
2 − 9a + 9 = 0, Δ = 9,
| | 3 | | 3 | |
a = |
| i b = 9 − 2* |
| = 6 lub a = 3 i b = 3 |
| | 2 | | 2 | |
 a=3 i h=3
albo
a= 3/2 i h=6
Jakby ktoś mógł to sprawdzić byłym wdzięczny
a=3 i h=3
albo
a= 3/2 i h=6
Jakby ktoś mógł to sprawdzić byłym wdzięczny 
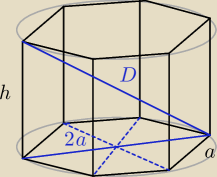 D = 3√5
D = 3√5
 Można tak rozwiązać: a > 0, b > 0
Można tak rozwiązać: a > 0, b > 0
