ostrosłup z rombem w podstawie bkc: Podstawą ostrosłupa jest romb o boku 20 cm, a pole jest równe 320 cm². Punkt przecięcia się przekątnych tego rombu jest spodkiem wysokości ostrosłupa. Wiedząc, że objętość ostrosłupa wynosi 1600 cm³, oblicz jego pole powierzchni bocznej. Bardzo proszę o rysunek.

sushi_ gg6397228: https://matematykaszkolna.pl/strona/995.html tutaj masz rysunek

bkc: Chodziło mi o rysunek, który zawierałby zaznaczoną wys. w rombie i wysokość ściany bocznej, bo takie wysokości pojawiają się w rozwiązaniu, ale nie umiem zaznaczyć tego na rysunku tak, żeby można było wszystko wyliczyć

Alfa:

bkc: Ja właśnie tak to widzę i nie wiem jaki to ma związek z zadaniem. Tzn w rozwiązaniu pojawia się połowa wys.podstawy²+H²=hsciany²

bkc: Wie ktoś jak rozwiązać?

Alfa:

	1
wg mnie to będzie raczej x =		a
	2

bkc: Wtedy nie zgadza się odpowiedź..( chyba, że ja coś źle liczę, wychodzi mi hs=5√13 ) Wg odpowiedzi ma być: hp = 16 cm H = 15 cm (te 2 mi się zgadzają)
hS = 17 cm Pb = 680 cm

Alfa: wg mnie dobrze policzyłeś h_s ja nie widzę błędu w tych obliczeniach, może ktoś inny spojrzy "świeżym okiem" i dostrzeże, gdzie jest błąd.

bkc: Ok. Dziękuję

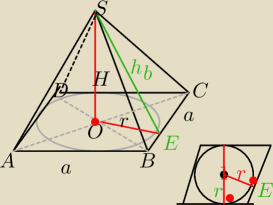
Mila: a=20 cm P_rombu=320 cm ² V_o=1600cm³

	1
Vo=		*Prombu*H
	3

	1
1600=		*320*H
	3

4800=320H

	4800
H=
	320

H=15 cm P_rombu=a*h 320=20*h h=16cm wysokość rombu

	1
r=		*16=8
	2

W Δ SOE: spodek wysokości h_b jest w punkcie styczności okręgu z bokiem rombu h_b²=r²+H² h_b²=8²+15² h_b²=64+225 h_b=17cm

	1
Pb=4*		*20*17
	2

P_b=2*20*17=680 cm²