trudny
martynka97: w trójkącie ABC dane są katy wewnetrzne :I ∡AI= 30 stopni , I∡BI=40 stopni. Oblicz miarę kąta:
a) miedzy dwusiecznymi kątów zewnetrznych, utworzonych przy wierzchołkach A i B
b) miedzy dwusieczna kata wewnetrznego ∡ A i dwusieczna kata zewnetrznego przy wierzchołku B.
c) miedzy prostymi zawierajacymi wysokosci opuszczone z wierzcholka A i z wierzchołka B.
d) miedzy prosta zawierajaca wysokosc poprowadzona z wierzchołka B i dwusieczna kata
zewnetrznego przy wierzcholku A.
16 lut 17:34
martynka97: pomocy
16 lut 17:39
martynka97: pomoze mi ktos to jest na jutro. a ja nie nawidze matematyki
16 lut 17:45
Alfa:
to jest proste zadanie
np. a)
∡C = 180
o − 30
o − 40
o = 110
o
α,β −> to kąty zewnętrzne trójkąta
α = 180
o − 30
o =
150o
β = 180
o − 40
o =
140o
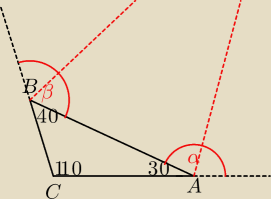
czerwone przerywane półproste, to dwusieczne kątów α i β. Tam, gdzie się przecinają (na
rys. ten punkt już się nie zmieścił), mamy szukany kąt, powiedzmy x.
Wówczas:
| | 1 | | 1 | |
x = 180o − ( |
| *150o + |
| *140o) = 180o − (75o + 70o) = 180o − 145o = 35o |
| | 2 | | 2 | |
pozostałe podpunkty robi się podobnie
16 lut 19:44