dowód
bezendu:
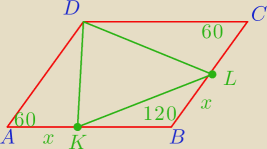
Kąt ostry rombu ABCD ma miarę |∡A | = 6 0
0 . Na bokach AB i BC wybrano punkty K i L w ten
sposób, że |AK | = |BL | . Uzasadnij, że trójkąt KLD jest trójkątem równobocznym
?
16 lut 17:19
Marcin: Akoro |AK|=|BL|, to Trójkąt DLC jest prostokątny

16 lut 17:21
bezendu: Już chyba wymyśliłem jakiś sposób.
16 lut 17:28
Marcin: No cieszę się

Tak w ogóle to siema

16 lut 17:30
5-latek: Wykaz z e albo wszystkie boki tego trojakt sa rownne lub ze katy tez sa rowne i maja po 60
stopni
MOzesz wykorzystac twierdzenie cosinusow dla trojkata AKD i trojkata KBL
\KB|=a−x
16 lut 17:32
bezendu:
|KD|2=|AD|2+|AK|2−2|AK|*|AD|*cos600
|KD|2=|AD|2+|AK|2−(|AK|*|AD|)
|KL|2=|KB|2+|AK|2−|AK|*KB|*cos1202
|KL|2=|KB|2+|AK|2+|AK|*BK|
I jednak nie mam dalej pomysłu.
16 lut 17:33
Mila:
CL=a−x
KB=a−x
I tw. cosinusów, jak to Ty lubisz.
16 lut 17:37
5-latek: np AK=x i AD=a i podstaw do 1 wzoru
16 lut 17:37
Marcin:
∡|AKD|=90°
∡|KDA|=180−90−60=30°
∡|LKB|=30°
∡|DKL|=180−∡|AKD|−∡|LKB|=180−90−30=60°
A nie można tak?
16 lut 17:42
Eta:
16 lut 17:45
5-latek: 
16 lut 17:46
Marcin: Czyli można

16 lut 17:47
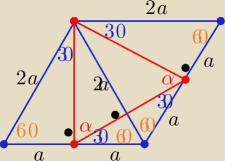
Eta:
trójkąt ma wszystkie kąty o równych miarach 60o
trójkąt ma wszystkie boki długości a√3
16 lut 17:48
bezendu:
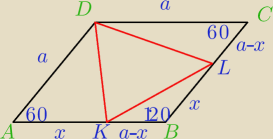
|KD|
2=a
2+x
2−2ax*cos60
0
|KD|
2=a
2+x
2−ax
|KL|
2=(a−x)
2+x
2−2(a−x)x*cos120
0
|KL|
2=a
2−2ax+x
2+ax
|KL|
2=a
2−ax+x
2
|LD|
2=a
2+(a−x)
2−2*a(a−x)*cos60
0
|LD|
2=a
2+a
2−2ax+x
2−a
2+ax
|LD|
2=a
2−ax+x
2
C.N.W
16 lut 17:51
Mila:
Dobrze.
Teraz zastanów się nad sposobem Ety.
16 lut 17:56
Eta:
Po co Ci tw. kosinusów? jakie własności ma romb?
Taki romb składa się z dwu trójkątów równobocznych o bokach długości
2a
Z własności trójkątów
ekierek 30
o,60
o, 90
o

16 lut 17:59
bezendu:
Bo zawsze jak wiedzę kąty i boki to tylko przychodzi mi na myśl tw.cosinusów.
16 lut 18:01
Eta:

16 lut 18:01
bezendu:
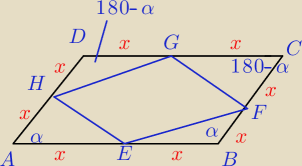
Wykaż, że środki boków rombu są wierzchołkami prostokąta.
Mogę w ten sposób zrobić korzystając z tw cos?
16 lut 18:05
bezendu:
Tylko ja muszę udowodnić, że czworokąt HEFG ma wszędzie kąt prosty. Tylko jak ?
16 lut 18:07
bezendu: ?
16 lut 19:06
Mila:
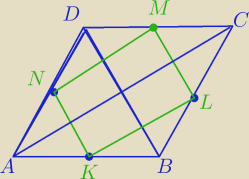
ML||DB,NK||DB
KL|AC,|NM||AC i AC⊥DB⇒? co?
16 lut 19:14
Eta:
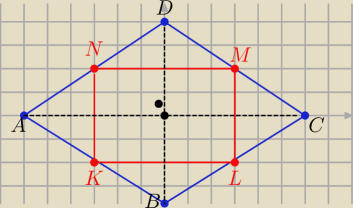
1/ odcinki łączące środki boków są odpowiednio równoległe do przekątnych rombu
2/ przekątne rombu są wzajemnie prostopadłe ⇒ odcinki są wzajemnie prostopadłe
Wniosek: czworokąt jest prostokątem
wniosek czworokąt jest prostokątem
16 lut 19:15
bezendu:
A z tego mojego nic by się nie dało zrobić ?
16 lut 19:17
5-latek: Ale nie udowodnil ze NK=ML i tak samo MN=KL
16 lut 19:17
Mila:
Tu trzeba wykorzystać prostopadłość przekątnych i równoległość do nich i związek z długością
przekątnych.
16 lut 19:58
bezendu: Postaram się to zapamiętać, choć już bardzo dużo tych dowodów się robi do zapamiętania
16 lut 19:59
5-latek: Milu a moze wykorzystac twierdzenienie o linii srodkowej trojakta ?
16 lut 20:02
bezendu:
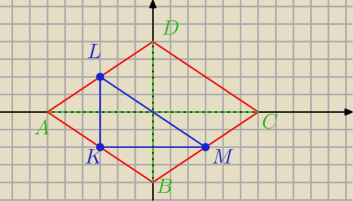
Na bokach AB , AD i BC rombu ABCD wybrano odpowiednio punkty K ,L i M w ten sposób, że
odcinki KL i KM są równoległe do przekątnych rombu. Wykaż, że odcinek LM przechodzi przez
punkt przecięcia przekątnych rombu
Trójkąt LKM jest prostokątny ale jak teraz resztę wykazać ?
16 lut 20:07
Mila:
To właśnie miałam na myśli 5− latku, ale nie podpowiadam wszystkiego, bo Bezendu, to
wie (mam nadzieję).
16 lut 20:27
bezendu: Znam to twierdzenie a odnośnie dowodu 20:27 ?
16 lut 20:31
Eta:
Jaki piękny rysunek

16 lut 20:35
bezendu:
Punktowany jest dowód a nie rysunek.
16 lut 20:36
Godzio:
Póki co nie powinien już przeszkadzać

16 lut 22:02
Marcin: Ktoś tu się bawi w admina

16 lut 22:02
bezendu: Dziękuję
Godzio 
16 lut 22:03
bezendu:
Ktoś ma jakiś pomysł jak dokończyć ?
16 lut 22:16
Eta:

16 lut 22:17
bezendu: ?
16 lut 22:25
Mila:
Skorzystaj z symetrii środkowej.
C =SO(A)
KL||BD , ΔAKL∼ΔABD −Δrównoramienne
|AL|=|AK|=oznx
Analogicznie
KB=BM=a−x⇔MC=x, LD=a−x⇔ M=SO(L)
16 lut 22:28
Mila: ⇔odcinek LM przechodzi przez
punkt przecięcia przekątnych rombu, który jest środkiem symetrii rombu.
16 lut 22:30
bezendu: Trzeba korzystać z tej symetrii środkowej ? Naprawdę nie można jakoś inaczej tego udowodnić ?
Bo ten sposób nie jest dla mnie zrozumiały
16 lut 22:31
Mila:
Wektory.
16 lut 22:32
bezendu:
To już chyba musi zostać ta symetria.
16 lut 22:34
Mila:
Oznacz na bokach rombu odcinki x i a−x i też wystarczy.
16 lut 22:38
Eta:
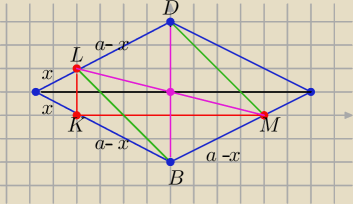
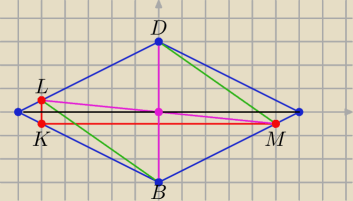
Jakim czworokątem jest czworokąt BMDL ?
i wszystko będzie jasne : przekątne tego czworokąta ......
16 lut 22:39
bezendu:
BMDL jest prostokątem
16 lut 22:41
Eta:

16 lut 22:47
bezendu:
Co ja piszę kwadratem
16 lut 22:48
Godzio:
No raczej też nie bo nie powstałby trójkąt ABL, miałby boki długości:
x,a,a − x
x + (a − x) > a sprzeczność
16 lut 22:51
Eta:
16 lut 22:52
bezendu: no to jest rombem
16 lut 22:53
Eta:
równoległobokiem
16 lut 22:53
Godzio:
No prawie ustrzeliłeś

16 lut 22:55
bezendu:
Strzelam bo nie wiem jak to dokończyć. A nie przejdę dalej dopóki nie zrozumiem
16 lut 22:57
Godzio:
To spróbuj uzasadnić, że jest to równoległobok, musisz jedynie wykazać, że LB || DM
16 lut 23:02
bezendu: jestem w kropce
16 lut 23:10
Godzio:
Może popatrz na odległości punktów L i M od wierzchołków.
16 lut 23:12
bezendu: Ta odległość jest równa
16 lut 23:13
Godzio:
No właśnie, to starczy, żeby były równoległe ?
16 lut 23:17
bezendu: Chyba tak. ?
16 lut 23:18
Eta:
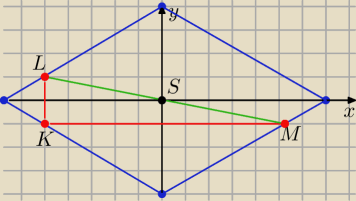
No to jeszcze tak:
Korzystając z "narzędzi" geometrii analitycznej
Umieść ten romb w układzie współrzędnych tak, by jego środek symetrii S (0,0)
M(x, −y), L( −x, y)
współczynnik kierunkowy prostej ML :
| | y+y | | −y | |
a= |
| = |
| ⇒ y=−ax −− zatem prosta ML przechodzi przez punkt S(0,0) |
| | −x−x | | x | |
co kończy dowód
16 lut 23:20
bezendu: I będzie ok jak tak napisze ?
16 lut 23:21
Godzio:
No starczy starczy

16 lut 23:22
bezendu: Dzięki w końcu to zrozumiałem do końca.
16 lut 23:23
Eta:
nie dopisałam :
..... tak,by jego środek symetrii S(0,0) i wierzchołki znajdowały się na osiach układu
16 lut 23:23
mietek: jestem

17 lut 09:08
 Kąt ostry rombu ABCD ma miarę |∡A | = 6 00 . Na bokach AB i BC wybrano punkty K i L w ten
sposób, że |AK | = |BL | . Uzasadnij, że trójkąt KLD jest trójkątem równobocznym
?
Kąt ostry rombu ABCD ma miarę |∡A | = 6 00 . Na bokach AB i BC wybrano punkty K i L w ten
sposób, że |AK | = |BL | . Uzasadnij, że trójkąt KLD jest trójkątem równobocznym
?

 Tak w ogóle to siema
Tak w ogóle to siema 



 |KD|2=a2+x2−2ax*cos600
|KD|2=a2+x2−ax
|KL|2=(a−x)2+x2−2(a−x)x*cos1200
|KL|2=a2−2ax+x2+ax
|KL|2=a2−ax+x2
|LD|2=a2+(a−x)2−2*a(a−x)*cos600
|LD|2=a2+a2−2ax+x2−a2+ax
|LD|2=a2−ax+x2
C.N.W
|KD|2=a2+x2−2ax*cos600
|KD|2=a2+x2−ax
|KL|2=(a−x)2+x2−2(a−x)x*cos1200
|KL|2=a2−2ax+x2+ax
|KL|2=a2−ax+x2
|LD|2=a2+(a−x)2−2*a(a−x)*cos600
|LD|2=a2+a2−2ax+x2−a2+ax
|LD|2=a2−ax+x2
C.N.W


 Wykaż, że środki boków rombu są wierzchołkami prostokąta.
Mogę w ten sposób zrobić korzystając z tw cos?
Wykaż, że środki boków rombu są wierzchołkami prostokąta.
Mogę w ten sposób zrobić korzystając z tw cos?
 ML||DB,NK||DB
KL|AC,|NM||AC i AC⊥DB⇒? co?
ML||DB,NK||DB
KL|AC,|NM||AC i AC⊥DB⇒? co?
 1/ odcinki łączące środki boków są odpowiednio równoległe do przekątnych rombu
2/ przekątne rombu są wzajemnie prostopadłe ⇒ odcinki są wzajemnie prostopadłe
Wniosek: czworokąt jest prostokątem
wniosek czworokąt jest prostokątem
1/ odcinki łączące środki boków są odpowiednio równoległe do przekątnych rombu
2/ przekątne rombu są wzajemnie prostopadłe ⇒ odcinki są wzajemnie prostopadłe
Wniosek: czworokąt jest prostokątem
wniosek czworokąt jest prostokątem
 Na bokach AB , AD i BC rombu ABCD wybrano odpowiednio punkty K ,L i M w ten sposób, że
odcinki KL i KM są równoległe do przekątnych rombu. Wykaż, że odcinek LM przechodzi przez
punkt przecięcia przekątnych rombu
Trójkąt LKM jest prostokątny ale jak teraz resztę wykazać ?
Na bokach AB , AD i BC rombu ABCD wybrano odpowiednio punkty K ,L i M w ten sposób, że
odcinki KL i KM są równoległe do przekątnych rombu. Wykaż, że odcinek LM przechodzi przez
punkt przecięcia przekątnych rombu
Trójkąt LKM jest prostokątny ale jak teraz resztę wykazać ?





 Jakim czworokątem jest czworokąt BMDL ?
i wszystko będzie jasne : przekątne tego czworokąta ......
Jakim czworokątem jest czworokąt BMDL ?
i wszystko będzie jasne : przekątne tego czworokąta ......



 No właśnie, to starczy, żeby były równoległe ?
No właśnie, to starczy, żeby były równoległe ?
 No to jeszcze tak:
Korzystając z "narzędzi" geometrii analitycznej
Umieść ten romb w układzie współrzędnych tak, by jego środek symetrii S (0,0)
M(x, −y), L( −x, y)
współczynnik kierunkowy prostej ML :
No to jeszcze tak:
Korzystając z "narzędzi" geometrii analitycznej
Umieść ten romb w układzie współrzędnych tak, by jego środek symetrii S (0,0)
M(x, −y), L( −x, y)
współczynnik kierunkowy prostej ML :

