Geometria Blue: Punkty A(2,3) i B(4,−1) sa dwoma kolejnymi wierzcholkami kwadratu ABCD. Wyznacz wpolrzedne pozostalych wierzcholkow tego kwadratu. Wiem jak to liczyć (tzn. tak mi się wydaje) Robię tak 1.liczę odległość między prostymi (wychodzi √10). 2. znajduję równanie prostej przechodzącej przez punkty a ib. 3. znajduje równanie prostej prostopadłej do prostej AB i przechodzącą przez punkt A 4. znajduje równanie prostej prostopadłej do prostej AB i przechodzącą przez punkt B 5. teraz znajduję ze wzoru na odległość punktów od siebie współrzędne punktów C i D D mi wychodzi, ale przy punkcie C delta mi wychodzi 32 i coś się nie zgadza:C Mógłby ktoś to wyliczyć tym sposobem co ja, bo liczę 3 raz i nie wiem, gdzie popełniam błąd ;c

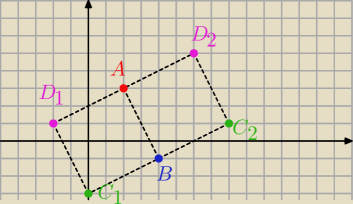
ICSP: 1. |AB| = 2√5 2. Oznaczam tą prostą jako l : −2x + 7

	1
3. Prosta prostopadła przechodząca przez punkt A, oznaczam jako k : y =		x + 2
	2

	1
4. Prosta prostopadła przechodząca przez punkt A, oznaczam jako k1 : y =		x − 3
	2

5. tego pkt niestety nie rozumiem, wzór na odległość dwóch punktów od siebie ? Nie jestem w 100% pewien ale chyba chodzi o coś takiego. Ustalmy pkt C tak aby był wierzchołkiem naprzeciw wierzchołka A. Zatem C(x_c ; y_c ) ∊ k₁ mamy :

	1		1
yc =		xc − 3, czyli C(xc ;		xc − 3)
	2		2

Wstawiając do do wzoru na długość odcinka :

	1
2√5 = √ (4 − xc)2 + (2 −		xc)2
	2

	1
20 = 16 − 8xc + xc2 + 4 − 2xc +		xc2
	4

5x_c² − 40x_c = 0 x_c = 0 v x_c = 8 C₁(0 ; −3) v C₂(8 ; 1)

	1
Teraz analogiczna operacja z pkt D(xd ;		xd + 2 )
	2

	1
√20 = √ (2 − xd)2 + (1 −		xd)2
	2

	1
20 = 4 − 4xd + xd2 + 1 − xd +		xd2
	4

5x_d² − 20x_d − 60 = 0 x_d² − 4x_d − 12 = 0 x_d = −2 v x_d = 6 D₁(−2; 1) v D₂(6 ; 5)

Blue: Już zauważyłam swój błąd, pomyliłam jedną cyferkę hehe