ostrosłup
Uczę się: Nie wiem czy jest już za późno, że nie myślę dobrze. Ale nie potrafię obliczyć długości
krawędzi trójkąta równobocznego w podstawie znając wysokość ściany bocznej (ostrosłup
prawidłowy trójkątny), 12 oraz kąt pomiędzy wysokością ściany bocznej i podstawy = 600.
resztę wyliczyłem tylko potrzebuje długości krawędzi.
16 lut 00:17
bezendu:
Napisz całe zadanie.
16 lut 00:23
Uczę się:
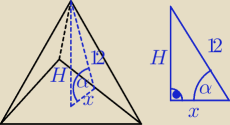
Dany jest ostrosłup prawidłowy trójkątny o wysokości ściany bocznej, której długość wynosi 12.
Ściana boczna tworzy z płaszczyzną podstawy kat 60
0. Oblicz objętność bryły.
Rysunek mój:
α=60
0
x=6
H=6
√3
16 lut 00:31
Uczę się: | | 1 | | 2 | |
czy to tutaj jest ta zależność, że wysokość ostrosłupa pada na |
| h lub |
| h  |
| | 3 | | 3 | |
16 lut 00:35
5-latek: Alez oczywiscie bo w podstawie tego ostroslupa jest trojkat rownoboczny
16 lut 00:37
Uczę się: obliczając tą krawędź podstawy powinienem z tej zależności skorzystać? kroczek po kroczku i się
w końcu uda ^^
16 lut 00:38
bezendu:
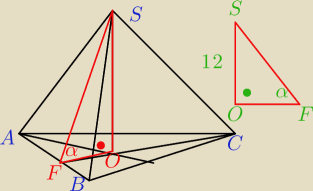
Do objętości będzie potrzebna podstawa więc:
tg60
0=
√3
√3|OF|=12
|OF|=4
√3
a
√3=24⇒a=8
√3
P
p=48
√3 j
2
V=192
√3 j
3
16 lut 00:41
Bogdan:
Hej bezendu, punkt F jest środkiem odcinka AB, ale na Twoim rysunku jest inaczej,
i bez urazy.
16 lut 00:47
Uczę się: bezendu, według odpowiedzi zrobiłeś źle
16 lut 00:47
bezendu: Ja się nie obrażam jak ktoś mi zwróci uwagę
Zraz jeszcze raz policzę.
16 lut 00:49
Uczę się: źle oznaczyłeś trójkąt. 12 to wysokość ściany bocznej a nie wysokość całej bryły.
16 lut 00:49
bezendu:
ja zrobiłem wysokość ostrosłupa 12 a w poleceniu, że wysokość ściany bocznej. Poprawię zaraz.
16 lut 00:50
Marcin: Uczę się rozwiązanie bezendu jest poprawne, tylko dane są inne. Zrób analogicznie i sprawdź
swój wynik
16 lut 00:51
Uczę się: Marcin przeciez widzę w odpowiedziach całkiem inne liczby, więc nie może być poprawne.
16 lut 00:52
Uczę się: aa, marcin sorka, faktycznie. chodziło ci o pomysł bezendu który jest dobry. właśnie analizuje
to co napisał.
16 lut 00:53
bezendu:
Według Twoich oznaczeń
2H=12
√3
H=6
√3
x
2=12
2−(6
√3)
2
x
2=36
x=6
U{a
√3{6}=6
a
√3=36
a=12
√3
P
p=108
√3 j
2
V=648j
3
16 lut 00:55
Uczę się: o i teraz jest dobrze, tylko czekaj niech spojrze na te obliczenia bo szukam w tym co napisałeś
gdzie obliczasz krawędź podstawy
16 lut 00:56
bezendu: Ja idę robić arkusze, potem pomogę jak coś.
16 lut 00:57
Uczę się: | | a√3 | |
co to za wzór |
| skąd to się wzieło? |
| | 6 | |
16 lut 00:57
Bogdan:
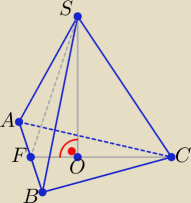
Staramy się rysować odcinek CF poziomo w ostrosłupie prawidłowym trójkątnym.
Wtedy kąt prosty FOS jest na rysunku też prosty.
16 lut 00:57
bezendu:
Dzięki za radę
Dobranoc.
16 lut 00:59
Uczę się: no faktycznie wychodzi wszystko, ale powie ktoś co to za wzór i skąd się wziął:
16 lut 01:00
Bogdan:
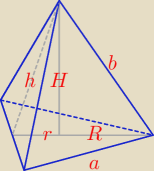
| | 1 | | 1 | | 1 | |
R = |
| a√3 = 2r, r = |
| a√3 = |
| R |
| | 3 | | 6 | | 2 | |
16 lut 01:00
Marcin: Może inaczej,
Skoro x=6, a wysokość w trójkącie równobocznym dzieli się 1:2, to h=18
Podstawiając do wzoru na wysokość trójkąta równobocznego:
16 lut 01:09
Uczę się: nie myślę. ja na dziś już skończę jutro pomyślę nad tym co napisałeś
16 lut 01:10
Marcin: Pewnie, ile można się uczyć
Pozdrawiam!
16 lut 01:14
Uczę się:
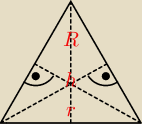
Ok, teraz już rozumiem. Dla przypomnienia inny rysunek:
16 lut 12:27