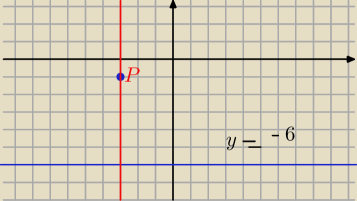
fkcja liniowa kwiatuszek: wyznacz równanie prostej przechodzącej przez pkt P(−3,−1) i prostopadłej do l l:y=−6 wiem jak to się robi... tylko pytanie. czym będzie to −6? a czy b?

bezendu: Napisz jak zrobiłeś

kwiatuszek: proszę, powiedz mi tylko gdzie to −6 podstawić

kwiatuszek: nie, jednak nie wiem jak to zrobić

5-latek:

bezendu:

kwiatuszek: tak, ale chodzi mi o to jak to rozwiązać... narysować to i ja umiem. nie wiem po prostu co podstawić gdzie do wzoru

kwiatuszek: ile tu wynosi 'a' a ile 'b'?

5-latek: Jaka to jest funkcja y=−6? Wiec ile wynosi a i b jesli wzor funkcji liniowej jest postaci y=ax+b ?

kwiatuszek: no a=0 a b = −6.... ale nie wychodzi mi to

kwiatuszek: i to jest f stała

Uczę się: P=(−3,−1) x y b=−6 y=ax+b −1=−3a−6 3a=−6+1

	−5
a=
	3

	−5
y=		x−6
	3

?

kwiatuszek: no nie... musi wyjść x=−3

Marcin: No i tyle wyjdzie

kwiatuszek: ale jak to obliczyc? proszę pomóżcie

Bogdan: prosta k₁: A₁x + B₁y + C₁ = 0 prosta k₂: A₂x + B₂y + C₂ = 0 Warunek prostopadłości: k₁ ⊥ k₂ ⇔ A₁A₂ + B₁B₂ = 0 W tym zadaniu: k₁: y + 6 = 0, A₁ = 0, B₁ = 1, C₁ = 6 k₂: A₂x + B₂y + C₂ = 0 i P(−3, −1)∊k₂, −3A₂ − B₂ + C₂ = 0 k₁ ⊥ k₂ ⇔ 0*A₂ + 1*B₂ = 0 ⇒ B₂ = 0, −3A₂ + C₂ = 0 ⇒ C₂ = 3A₂ dla B₂ = 0 i C₂ = 3A₂ k₂: A₂x + 3A₂ = 0 ⇒ x = −3 i A_a≠0 Odp.: x = −3 Najprościej jednaj jest od razu zauważyć, że prosta prostopadła do prostej y = −6 i przechodząca przez punkt (−3, 1) ma równanie x = −3.

kwiatuszek: dziękuję! <3

kwiatuszek: ech...tylko nie rozumiem tych oznaczeń a1, a2 itd...