Zadania ze stereometrii
polonista: Hej.
Pomożecie mi z trzema zadaniami ze stereometrii?
Zad. 1
Graniastosłup prawidłowy trójkątny przecięto płaszczyzną przechodzącą przez krawędź podstawy i
przecinającą krawędzie przeciwległej podstawy w odległości 2/3 od ich wspólnego wierzchołka.
Oblicz pole otrzymanego przekroju oraz cosinus jego kąta nachylenia do płaszczyzny podstawy.
Długość krawędzi podstawy wynosi a=9cm a wysokość graniastosłupa h=6cm.
Zad. 2
W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość \alpha a kąt przy
wierzchołku między krawędziami bocznymi wynosi \alpha. Oblicz:
a) Ppc tego ostrosłupa
b) Pp przekroju płaszczyzna przechodząca przez wierzchołek ostrosłupa i przekątna podstawy
c) Tangens kąta nachylania krawędzi bocznej do płaszczyzny podstawy
Zad. 3
W ostrosłup prawidłowy trójkątny wpisano stożek. Krawędź boczna ma długość b, kąt przy płaskim
wierzchołku ostrosłupa jest równy \alpha. Oblicz Ppc i V stożka.
Nie dość, że trudne to dziwnie sformułowane. Taką mam nauczycielkę

Pomóżcie, proszę.
 Pomóżcie, proszę.
Pomóżcie, proszę.
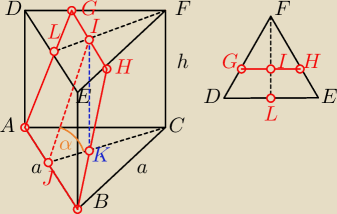 a = 9
h = 6
KI = h = 6
FD = FE = DE = a = 9
a = 9
h = 6
KI = h = 6
FD = FE = DE = a = 9
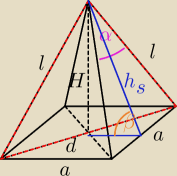 dane: a, α
a2 = 2l2 − 2l2 cosα
l =
hs = √l2 − (a2)2 =
H = √hs2 − (a2)2 =
d = a√2
Pc = a2 + 2a*hs =
dane: a, α
a2 = 2l2 − 2l2 cosα
l =
hs = √l2 − (a2)2 =
H = √hs2 − (a2)2 =
d = a√2
Pc = a2 + 2a*hs =
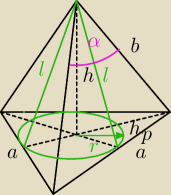 dane: b , α
a2 = 2b2 − 2b2cosα
a =
l = √b2 − (a2)2 =
dane: b , α
a2 = 2b2 − 2b2cosα
a =
l = √b2 − (a2)2 =
