jw magda: W jakim stosunku przecina się wysokość w trójkącie równoramienny opadająca na podstawę

Bogdan: O co chodzi? Podaj dokładnie treść zadania.

J: Chodzi chyba o trójkąt równoboczny

magda: W rownobocznym wiem jak się dzieli. Ale czy jest jakaś zależność w trójkącie równoramienny. Czy wysokości przecinają się w jakimś stosunku?

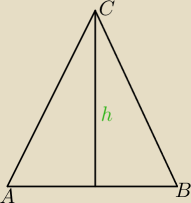
5-latek: Wysokosc w trojkacie rownoramiennym wychodzaca z wierczcholka C dzieli podsatwe na polowe W trojkacie rownoramiennym wysokosc ta jest jednoczesnie srodkowa ,i dwusieczna kata C

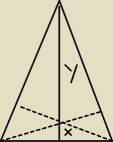
magda: Jest zaleznosc miedzy x i y?

PW: W każdym trójkącie wysokości przecinają się dzieląc każdą z nich w stosunku 2:1 licząc od wierzchołków.

J: Zależności generalnej ,takiej jak w trójkącie równobocznym nie ma. Mogą być różne zależności,ale wynikające z treści konkretnego zadania.

Marcin: PW serio w każdym?

J: Witam "PW" Skąd takie twierdzenie ?

PW: Pomyliłem twierdzenia. Biję się w piersi − to twierdzenie o środkowych trójkata! I myli mi się to cholerstwo od dzieciństwa. Przepraszam.

J: "Mylić się" jest rzeczą ludzką, "sztuką" przyznać się do błędu

Marcin:

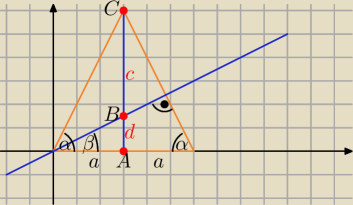
Bogdan: Można znając miarę kąta α wyprowadzić taką zależność: β = 90^o − α, a > 0 A = (a, 0), B = (a, a*tgβ) = (a, a*tg(90^o − α)) = (a, a*ctgα), C = (a, a*tgα}

c		a*(tgα − ctgα)		tgα − ctgα
	=		=
d		a*ctgα		ctgα

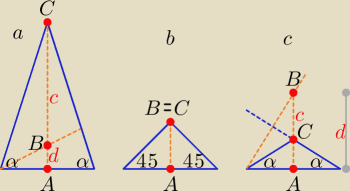
Bogdan: c = |BC|, d = |AB|, punkt B to ortocentrum trójkata kontynuując otrzymujemy: a. dla α ∊ (45^o, 90^o):

	c		tgα − ctgα		tgα		tg2α − tgα ctgα
		=		*		=		= tg2α − 1
	d		ctgα		tgα		tgα ctgα

	c
b. dla α = 45o:		= 0
	d

	c
c. dla α ∊ (0o, 45o):		= 1 − tg2α
	d

	c
Można ująć wszystkie wymienione przypadki zależnością:		= |tg2α − 1|
	d