Kombinatoryka Seb: Oblicz prawdopodobieństwo, że przy losowaniu 5 kart z talii 52 kart wylosujemy co najmniej dwa króle i jednego asa.

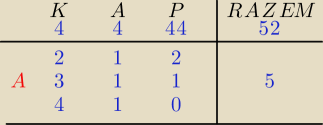
Bogdan: K − króle, A − asy, P − pozostałe

	52 5
|Ω| =

	4 2		4 1		44 2		4 3		4 1		44 1		4 4		4 1		44 0
|A| =		*		*		+		*		*		+		*		*

	|A|
P(A) =
	|Ω|

Seb: oj w treści zadania powinno być co najmniej jednego asa, a nie tylko jednego

Bogdan: Wobec tego masz rozwiązanie dla jednego asa, rozwiąż swoje zadanie analogicznie do tego rozwiązania.

Ajtek: Witaj Bogdan . Seb masz sposób rozwiązania zadania, wysil się trochę. Znikam na hokej.

Marcin: Masz po prostu więcej przypadków do rozpatrzenia dla |A|. Skorzystaj z tego, co napisał Bogdan

Bogdan: Można rozpatrzyć zdarzenie: co najmniej dwa króle i brak asów

Bogdan: Witaj Ajtek

Seb: Mógłby ktoś policzyć A? Bo mi wychodzi 6 przypadków i 25044

Seb: Halo? Ponawiam pytanie.