$%$%
qu:
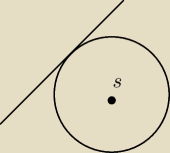
prosta ma równanie y=5x −3
S= (2,8)
napisz równanie okręgu stycznego do równaniu o prostej
14 lut 23:25
Saizou :
d=r i działaj
14 lut 23:26
wredulus_pospolitus:
a jak nie znasz wzoru na odległość ... to 'na chama' :
(x−2)
2 + (y−8)
2 = r
2
y=5x−3
rozwiązujesz ten układ.
Równianie kwadratowe −−− ma mieć 1 rozwiązanie (czyli Δ=0) ... dla jakiej wartości parametru
'r' będzie to spełnione
14 lut 23:30
Fleur: 
Dla Artura
14 lut 23:39
qu: 3√1313
wychodzi kosmos ale licze od nowa ..........
14 lut 23:42
Eta:
k: 5x−y−3=0 S(2,8)
Odległość środka S od prostej k jest d=r
| | |2*5−1*8−3| | |
r=d= |
| = ....... ⇒ r2=.... |
| | √25+1 | |
o: (x−2)
2+(y−8)
2= r
2
14 lut 23:47
qu: r
2 =
126
licznik 10−8−3= |1|
mianownik P{26}
do kwadratu ?
14 lut 23:52
Eta:
tak
14 lut 23:53
qu: (x−2)2 + (y−8)2= 126
tak ?
15 lut 00:00
Eta: ok
15 lut 00:02
wredulus_pospolitus:
a 'na chama' by było:
(x−2)
2 + (5x−11)
2 = r
2
x
2−2x+4 + 25x
2 − 110x + 121 = r
2
26x
2 − 114x + 125 − r
2 = 0
| | 1 | |
Δ = 12'996 − 13'000 + 104r2 = − 4 + 104r2 = 0 <=> r2 = |
| |
| | 26 | |
15 lut 00:25