geooometria płaska-trójkąty Kubaa :): Siemanko, to znowu ja, ale mam problem z zadankiem: Dany jest trójkąt rozwartokątny równoramienny, którego boki mają długość 16 cm, 10 cm, 10 cm. Wyznacz promień okręgu wpisanego w ten trójkąt oraz promień okręgu opisanego na tym trójkącie. Chętny ktoś pomóc?

ICSP: Najpierw policz pole trójkąta.

Kubaa :): P=1/2ah ? To ten wzór? Jeśli tak, to skąd mam wiedzieć, która liczba to a, i jak wyliczyć h?

ICSP: to trójkąt równoramienny ! W trójkącie równoramiennym wysokość poprowadzona z wierzchołka(przy ramionach o tej samej długosci) przecina podstawę(najdłuższy bok) dokładnie w połowie. Zrób rysunek, policz wysokość, później ze wzoru.

Kubaa :): Dobra, sorry, wieczór jest i już nie myślę, ale ok, wyszło mi, że h=6 pole trójkąta=30

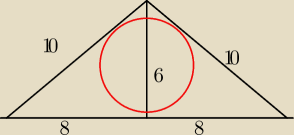
Janek191: h² = 10² − 8² = 100 − 64 = 36 h = √36 = 6 Pole Δ P = 0,5 a*h = 0,5*16*6 = 48 Obwód Δ L = 2*10 + 16 = 36 r − promień okręgu wpisanego P = 0,5 L*r

	2 P		2*48		96		8		2
r =		=		=		=		= 2
	L		36		36		3		3

	2
r = 2		cm
	3

============= R − promień okręgu opisanego Korzystamy z wzoru

	a*b*c		a*b*c
P =		⇒ R =
	4 R		4 P

czyli

	16*10*10		1 600		1
R =		=		= 8
	4*48		192		3

	1
R = 8		cm
	3

=============

Kubaa :): Czyli a=16 xD, ok rozumiem, dzięki za wyrozumiałość i pomoc