123

123 qu: W trapezie ABCD ramiona mają długość |AD| = 10 oraz |BC|=17, zaś tangens kąta nachylenia ramienia AD do dłuższej podstawy wynosi ⁴₃. Oblicz pole trójkąta DBC, jeśli wiadomo, że w dany trapez można wpisać okrąg

14 lut 21:35

Eta:

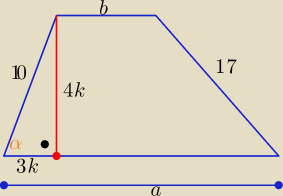
1/ z warunku wpisania okręgu w trapez : a=b=10+17 = 27

	4k
2/ tgα=		, k>0
	3k

16k²+9k²=100 ⇒ k= 2 to h= 4k = 8

	a+b
P=		*h=..........
	2

14 lut 21:47

Eta: Poprawiam chochlika : w 1/ a+b=10+17=27

14 lut 21:59

qu: Wyjedzie pole trapezu a mi potrzebne pole trójkąta DBC

14 lut 22:03

Hajtowy: DA = przekątna trapezu = przeciwprostokątna trójkąta szukanego

14 lut 22:08

Hajtowy: Trochę wyobraźni mistrzu!

14 lut 22:08

qu:

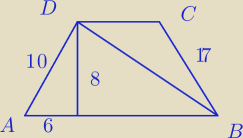
p=108 mam obliczyć pole DBC

14 lut 22:30

qu: DA wg mnie to nie jest przekątna trapezu tylko ramię

14 lut 22:51

wredulus_pospolitus: qu: 1) 'puszczasz' wysokość z C 2) wyliczasz odcinek 'przecięcie' − B (tw. Pitagorasa) 3) stosujesz tw. o którym pisałem w tamtym zadaniu (suma przeciwległych boków jest sobie równa) 4) wyznaczasz DC ... a dzięki temu także AB 5) obliczasz pole 6) koooniec

14 lut 22:55