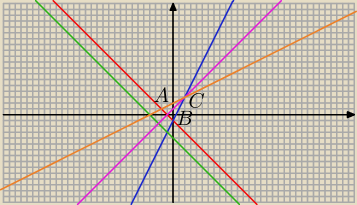
 x + y + 1 = 0 ⇒ y = − x − 1 ( na rysunku prosta czerwona )
2 x − y − 1 = 0 ⇒ y = 2 x − 1 ( na rysunku prosta niebieska )
P = ( − 4; 0 ) − leży na prostej k
Mamy
− x − 1 = 2 x − 1
3 x = 0
x = 0
y = 2*0 − 1 = −1
więc
B = ( 0; − 1) − punkt przecięcia się prostych
=========
Przez punkt P = ( − 4 ; 0 ) prowadzę prostą równoległą do prostej o równaniu y = − x − 1
y = − x + b1
0 = − ( −4) + b1 ⇒ b1 = − 4
y = − x − 4 ( na rysunku prosta koloru zielonego )
========
Znajduję punkt wspólny prostych o równaniach y = − x − 4 i y = 2 x − 1
− x − 4 = 2 x − 1
3x = − 3
x = − 1
y = 2*( − 1) − 1 = − 3
P1 = ( − 1; − 3)
============
Znajduję środek S odcinka P P1 ; P = ( − 4; 0) ,
S = ( − 2,5 ; − 1,5 )
===============
Przez punkt S prowadzę prostą prostopadłą do prostej AB ( y = − x − 1 )
− 1* a2 = − 1 ⇒ a2 = 1
y = x + b2
−1,5 = −2,5 + b2 ⇒ b2 = 1
y = x + 1 ( na rysunku prosta koloru różowego )
========
Proste o równaniach y = x + 1 i y = 2x − 1 ( BC ) przetną się w punkcie C
x + 1 = 2 x − 1
x = 2
y = 2*2 − 1 = 3
C = ( 2; 3)
========
Prosta PC
P = ( − 4; 0)
y = a x +b
0 = − 4a + b
3 = 2a + b
−−−−−−−−−−−−−−−−−−−−−
3 = 6a
a = 0,5
b = 3 − 2a = 3 − 2*0,5 = 2
y = 0,5 x + 2 ( na rysunku prosta koloru pomarańczowego − prosta k )
==========
Przetnie się ona z prostą o równaniu y = − x − 1 w punkcie A
0,5 x + 2 = − x − 1
x + 4 = −2 x − 2
3 x = − 6
x = − 2
y = 0,5*(−2) + 2 = 1
A = ( − 2; 1)
==========
Odp. k : y = 0,5 x + 2
=======================
x + y + 1 = 0 ⇒ y = − x − 1 ( na rysunku prosta czerwona )
2 x − y − 1 = 0 ⇒ y = 2 x − 1 ( na rysunku prosta niebieska )
P = ( − 4; 0 ) − leży na prostej k
Mamy
− x − 1 = 2 x − 1
3 x = 0
x = 0
y = 2*0 − 1 = −1
więc
B = ( 0; − 1) − punkt przecięcia się prostych
=========
Przez punkt P = ( − 4 ; 0 ) prowadzę prostą równoległą do prostej o równaniu y = − x − 1
y = − x + b1
0 = − ( −4) + b1 ⇒ b1 = − 4
y = − x − 4 ( na rysunku prosta koloru zielonego )
========
Znajduję punkt wspólny prostych o równaniach y = − x − 4 i y = 2 x − 1
− x − 4 = 2 x − 1
3x = − 3
x = − 1
y = 2*( − 1) − 1 = − 3
P1 = ( − 1; − 3)
============
Znajduję środek S odcinka P P1 ; P = ( − 4; 0) ,
S = ( − 2,5 ; − 1,5 )
===============
Przez punkt S prowadzę prostą prostopadłą do prostej AB ( y = − x − 1 )
− 1* a2 = − 1 ⇒ a2 = 1
y = x + b2
−1,5 = −2,5 + b2 ⇒ b2 = 1
y = x + 1 ( na rysunku prosta koloru różowego )
========
Proste o równaniach y = x + 1 i y = 2x − 1 ( BC ) przetną się w punkcie C
x + 1 = 2 x − 1
x = 2
y = 2*2 − 1 = 3
C = ( 2; 3)
========
Prosta PC
P = ( − 4; 0)
y = a x +b
0 = − 4a + b
3 = 2a + b
−−−−−−−−−−−−−−−−−−−−−
3 = 6a
a = 0,5
b = 3 − 2a = 3 − 2*0,5 = 2
y = 0,5 x + 2 ( na rysunku prosta koloru pomarańczowego − prosta k )
==========
Przetnie się ona z prostą o równaniu y = − x − 1 w punkcie A
0,5 x + 2 = − x − 1
x + 4 = −2 x − 2
3 x = − 6
x = − 2
y = 0,5*(−2) + 2 = 1
A = ( − 2; 1)
==========
Odp. k : y = 0,5 x + 2
=======================

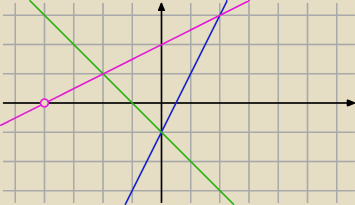 wykorzystaj wzór na tangens kąta między prostymi
(policzysz tgφ między danymi prostymi tgφ=3 ... a potem wyznaczysz wsp. kierunkowy
prostej nachylonej do prostej x+y+1=0 pod takim samym kątem.
Otrzymasz a=2 (odrzucisz) lub a=1/2
wykorzystaj wzór na tangens kąta między prostymi
(policzysz tgφ między danymi prostymi tgφ=3 ... a potem wyznaczysz wsp. kierunkowy
prostej nachylonej do prostej x+y+1=0 pod takim samym kątem.
Otrzymasz a=2 (odrzucisz) lub a=1/2
| 1 | ||
Znając a=1/2 i P=(−4, 0) napiszesz k: y= | x+2 | |
| 2 |