 :
1. W trójkącie prostokątnym ABC wysokość CD poprowadzona z wierzchołka kąta prostego podzieliła
przeciwprostokątną AB na odcinki długości 9 cm i 1 cm. Oblicz:
a) |CD|
b) długość odcinka symetralnej boku AB zawartego w tym trójkącie.
W tym zadaniu, zrobiłem podpunkt a, ale mam problem z ułożeniem talesa do punktu b,
2. W trójkącie równoramiennym ABC boki mają długość: |AC| = |BC| = 10 cm, |AB| = 16 cm. Punkty
D, E są odpowiednio środkami ramion AC i BC tego trójkąta. Wyznacz obwód trójkąta AED.
W tym zadaniu obliczyłem długość odcinka DE, DE=1/2AB
:
1. W trójkącie prostokątnym ABC wysokość CD poprowadzona z wierzchołka kąta prostego podzieliła
przeciwprostokątną AB na odcinki długości 9 cm i 1 cm. Oblicz:
a) |CD|
b) długość odcinka symetralnej boku AB zawartego w tym trójkącie.
W tym zadaniu, zrobiłem podpunkt a, ale mam problem z ułożeniem talesa do punktu b,
2. W trójkącie równoramiennym ABC boki mają długość: |AC| = |BC| = 10 cm, |AB| = 16 cm. Punkty
D, E są odpowiednio środkami ramion AC i BC tego trójkąta. Wyznacz obwód trójkąta AED.
W tym zadaniu obliczyłem długość odcinka DE, DE=1/2AB


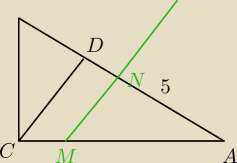
| ICDI | IMNI | ||
= | , bo symetralna dzieli bok AB na pół. | ||
| 9 | 5 |
 h2 + 122 = d2
h2 + 122 = d2
 , dzięki za pomoc
, dzięki za pomoc