Funkcja, planimetria Zuzu: Przy odpowiednich założeniach p i q, wykaż że jeżeli w rombie suma długości przekątnych wynosi

	1
p, a suma długości kwadratów tych przekątnych q, to pole rombu wynosi		(p2−q). Proszę o
	4

pomoc jak to rozwiązać

Zuzu: Proszę o pomoc

J: a+b = p ; a² + b² = q , gdzie a i b to przekatne.

1		1		1
	(p2 − q) =		[ (a + b)2 − (a2 + B2)] =		[a2 + 2ab + b2 −a2 − b2]
4		4		4

	1		1
=		(2ab) =		*a*b = Pole rombu
	4		2

Aga1.: e+f=p e²+f²=q f=p−e e²+p²−2pe+e²=q 2e²−2pe+p²−q=0 oblicz e Δ=4p²−8(p²−q)=4p²−8p²+8q=8q−4p²=4(2q−p²) √Δ=2√−p²+2q

	2p+2√−p2+2q
e1=		=
	4

f=

	e*f
A pole P=
	2

5-latek: Czesc J czyba pokazales w druga strone ?

Aga1.: J ,Twój sposób jest krótszy.

Zuzu: dziękuję.

Bizon: a+b=p ⇒ a²+2ab+b²=p² a²+b²=q a² +b²=q 2ab =p²−q a pole rombu to:

	1		1
S=		ab zatem: S=		(p2−q)
	2		4

J: Cześć Na to samo wychodzi ... L = P

Zuzu: Mam jeszcze jedno zadanie, które wydaje się banalnie proste ale już zgłupiałam czy tak ma wyglądać. Treść : W mieszkaniach pewnego bloku mieszkają odpowiednio: 4, 2, 2, 6, 3, 1, 5, 5, 3, 3, 6, 1, 4, 2, 2, 4, 5, 2, 1, 6, 3, 5, 2, 1, 2 osoby. przedstaw te dane w postaci diagramu w ukłądzie współrzędnych, gdzie oś pozioma to liczba osób, a oś pionowa to liczba mieszkań zamiszkiwanych przez dane osoby. Jak to powinno wyglądać?

J: Na osi poziomej zaznaczasz punkty 1,2,3,4,5,6 , an osi pionowej w ilu mieszkaniach zmieszkuje 2 osoba, w ilu dwie osoby , itd ...( np. 6 osób zamieszkuje w 3 mieszkaniach)

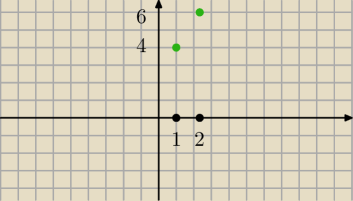
J: Przykład: 1 osoba w 4 mieszkaniach, 2 osoby w 6 −ciu itd

Zuzu: