Zadanka 5-latek: Lap Saizou W kolo o promieniu R wpisano 3 jednakowe kola styczne wewnetrznie do danego kola . . kazde z tych 3 kol jest stycznie zewnetrznie do do dwoch pozostalych . Dookola srodka danego kola powstala pewna figura ograniczona trzema lukami kol wpisanych. Oblicz pole tej figury .

5-latek: i drugie W czwroscianie ABCD odcinek KL laczacy srodek K krawedzi AB ze srodkiem L krawedzi CD jest prostopadaly zarowno do AB jak i do CD , przy czym odcinek CD jest prostopadly do plaszczyzny ABL. Obliczyc promien kuli wpisanej w czworoscian gdy dane sa jego odcinki AB=a CD=b KL=w Trzecie

	1
Rozwiaz rownanie sinx*sin3x =		podajac wszystkie mzliwe rozwiazania .
	2

Tyle na razie

Saizou : może na zaś, bo teraz mi się nie chce

5-latek: OK

Saizou :

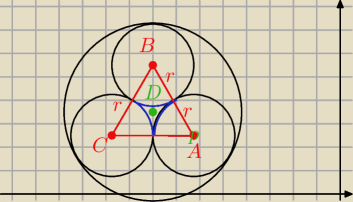
	60		1
Pniebieskie=PABC−3*		*πr2=r2(√3−		π)
	360		3

punkt D jest środkiem ciężkości ΔABC

	2	r√3		√3
AD=			=		r
	3	2		3

AD=R−r

	√3
R−r=		r
	3

3R−r=√3r 3R=(√3+1)r

	3(√3−1)
r=		R
	4

	9(4−2√3)		1
P=		(√3−		π)R2
	16		3

czy jakoś tak

5-latek: Odpowiedz to

	pi
S=3(7−4√3)*(√3−		)*R2
	2