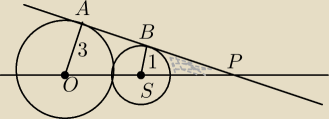
pomocy abcd: Okrąg o środku O i promieniu 3 jest styczny zewnętrznie do okręgu o środku S i promieniu 1. Prosta przechodząca przez środki tych okręgów przecina sprostą styczną do obu okręgów w punkcie P. Oblicz miarę kąta BSP oraz pole zacieniowanego obszaru.

wredulus_pospolitus: znasz odcinek |OS| = 3+1 = 4 z Tw. Talesa wyznaczasz |PS| = ... wiesz że Δ_PBS jest prostokątny (wyjasniac chyba nie musze dlaczego to wiesz), w takim razie:

	|BS|
cos (∡BSP) =		= ....
	|PS|

i stąd wyznaczasz miarę tego kąta

J: Pole zakreskowanej figury: P = PΔ_BPS − pole wycinka koła o promieniu 1 i kącie BSP

abcd: A jak z Talesa wyznaczyć to |PS| Co mam podstawić?

abcd:

abcd: Podpowie ktoś

J:

3		1
	=		⇔ 3PS = 4 + PS ⇔ 2PS = 4 ⇔ PS = 2
4 + PS		PS

abcd: Dzięki