Dowód, proszę o pomoc. Zuzu:

	a2		b2		6a2−12a+8
Udowodnij, że jeżeli a+ b = 2 to		+		=
	b		a		a(2−a)

wredulus_pospolitus: a+b=2 <=> b = 2−a stąd:

a2		b2		a3+b3		a3 + (2−a)3
	+		=		=
b		a		ab		a*(2−a)

(2−a)³ = .... wzór skróconego mnożenia i co otrzymujesz trudne było

Zuzu: Nie, nie było Dziękuję. Pomożesz mi z następnym?

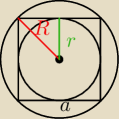
Zuzu: Pole pierścienia kołowego ograniczonego okęgami wpisanymi i opisanymi na kwadracie równa się 4π. Oblicz pole kwadratu.

Zuzu: Wyszło mi, że pole wynosi 16, dobrze?

kaka:

	1		1
Pole pierscienia PK−Pk gdzie R=		d r=		a d=a√2
	2		2

Zuzu: czyli wynik się zgadza, prawda?

wredulus_pospolitus: π(R²−r) = 4π −> R²−r² = 4 −> 2a²−a² = 16 −> a²=16 ... tak ... zgadza się

Zuzu: dziękuję