matematykaszkolna.pl
całki powierzchniowe olla: ∫∫s (4x + y) ds ,gdzie s jest powierzchnią x=√4−y2 dla 0≤ z ≤1 czy może mi ktoś pomóc i wytłumaczył krok po kroku jak się robi takie zadania?
13 lut 23:55
olla:
14 lut 00:11
Ada: To jest całka nieskierowana Jak się zmienia x
14 lut 00:15
olla: emotka nie mam pojęcia, proszę o wytłumaczenie. tak na pewno jest nieskierowana.
14 lut 00:27
olla: wytłumaczy ktoś
14 lut 00:42
Ada: rysunekx(y,z)=√4−y2 I = ∫∫SF(x,y,z) dS = ∫∫DF(x(y,z),y,z)*√1+f'2y+f'2z dydz F(x(y,z),y,z) = 4√4−y2+y z∊[0,1] y∊[−2,2] I=∫−22 dy ∫014√4−y2+y dz = ∫−224√4−y2+y dy = ...
14 lut 00:52
Ada: Ach, nie pomnożyłam całki przez √1+(x'z)2+(x'y)2 x'z=0
 −2y 
x'y=
 4−y2 
 4−y2+4y2 4−3y2 
√
=p{
 4−y2 4−y2 
 4−3y2 
I=∫−22 dy ∫01 (4√4−y2+y)(p{
) dz
 4−y2 
 4−3y2 
= ∫−22(√4−3y2+yp{
)[z]10 dy =
 4−y2 
 4−3y2 
∫−22(√4−3y2+yp{
)dy=...
 4−y2 
14 lut 00:58
olla: dziękuje Ada, muszę to dokładnie przejrzeć
14 lut 01:05
olla: najgorsze jest chyba to że mam problem z obszarami, bo reszta to już tylko do wzoru podstawićemotka
14 lut 01:05
olla: a mam pytanko, jak tam mam ten x=.... więc dlatego liczę całkę dy dz a jeśli miałabym np podane że y =.... to bym liczyła całkę z dxdz dobrze rozumiem?
14 lut 01:09
Trivial: Ależ po co wykonywać takie karkołomne obliczenia... Stosujemy przejście na współrzędne walcowe.
 ⎧x = Rcosφ 
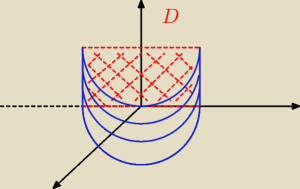
⎨y = Rsinφ (φ,z)∊[−π2,π2]×[0,1] = D
 ⎩z = z 
Wektor normalny dla takiego przekształcenia jest n = (Rcosφ, Rsinφ, 0) → ||n|| = R Wstawiamy do całki (R = 2): ∬S(4x+y)dS = ∬D(8cosφ+2sinφ)*2dφdz = [16sinφ−4cosφ]−π/2π/2 = 32.
14 lut 19:37