 Zadanie z egzaminu. Chodzi o to jakie trzeba tu dopisać komentarze, żeby było dobrze.
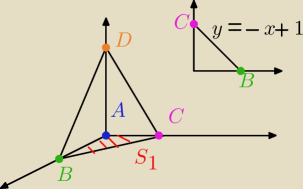
Niech S będzie powierzchnią boczna ostrosłupa o wierzchołkach ABCD o podstawie ABC, gdzie
A=(0,0,0), B=(1,0,0), C=(0,0,1) i D=(0,0,2). Oblicz strumień pola wektorowego F=(x, −y, z2)
przez wewnętrzną stronę powierzchni S.
Powierzchnia boczna ostrosłupa składa się z trzech trójkątów, ostrosłupa bez podstawy. Można
korzystając z twierdzenia Gaussa−Ostrogradskiego policzyć strumień całego ostrosłupa (jego
powierzchnia jest zamknięta) i odjąć strumień przechodzący przez podstawę.
Twierdzenie Gaussa zakłada, że powierzchnia zorientowana jest zewnętrznie, z tym, że istnienie
jednej całki (zorientowanej np. zewnętrznie) implikuje istnienie drugiej całki. Są one sobie
równe co do wartości, mają jednak przeciwnie skierowane znaki.
Więc:
S−powierzchnia całego ostrosłupa.
I1=∫∫S−=−∫∫∫VdivFdV
Zadanie z egzaminu. Chodzi o to jakie trzeba tu dopisać komentarze, żeby było dobrze.
Niech S będzie powierzchnią boczna ostrosłupa o wierzchołkach ABCD o podstawie ABC, gdzie
A=(0,0,0), B=(1,0,0), C=(0,0,1) i D=(0,0,2). Oblicz strumień pola wektorowego F=(x, −y, z2)
przez wewnętrzną stronę powierzchni S.
Powierzchnia boczna ostrosłupa składa się z trzech trójkątów, ostrosłupa bez podstawy. Można
korzystając z twierdzenia Gaussa−Ostrogradskiego policzyć strumień całego ostrosłupa (jego
powierzchnia jest zamknięta) i odjąć strumień przechodzący przez podstawę.
Twierdzenie Gaussa zakłada, że powierzchnia zorientowana jest zewnętrznie, z tym, że istnienie
jednej całki (zorientowanej np. zewnętrznie) implikuje istnienie drugiej całki. Są one sobie
równe co do wartości, mają jednak przeciwnie skierowane znaki.
Więc:
S−powierzchnia całego ostrosłupa.
I1=∫∫S−=−∫∫∫VdivFdV
| ∂ | ∂ | ∂ | ||||
divF=[ | , | , | ]•[x, −y, z2]= | |||
| ∂ x | ∂ y | ∂ z |
| 1 | ||
−8∫01 [(1−x)3−(1−x)3+ | (1−x)3]dx=−3∫01(1−2x+x2)dx= | |
| 3 |
| 1 | 1 | |||
−3[x−x2+ | x3]10=−3[1−1+ | ]=−1 | ||
| 3 | 3 |
