plani
bezendu:
Zadanie
Ma ktoś jakieś zadnia na podobieństwo, przystawanie trójkątów ?
13 lut 20:19
Hajtowy:
Zadanie 1
W urnie jest 2 razy więcej kul czarnych niż białych i 3 razy więcej kul zielonych niż białych.
Przy losowaniu 3 kul z tej urny prawdopodobieństwo wylosowania 3 kul różnych kolorów wynosi
| | 27 | |
|
| . Jakie jest prawdopodobieństwo wylosowania z urny 3 kul, wśród których dokładnie 2 |
| | 136 | |
będą tego samego koloru
Zadanie 2
Z pojemnika, w którym jest n kul białych i 2n kul czarnych n ≥ 3 wybieramy losowo jednocześnie
3 kule. Oblicz prawdopodobienstwo zdarzenia A − otrzymamy co najmniej 2 kule biale
13 lut 20:25
Hajtowy: Oj.... przeczytałem prawdopodobieństwo


ale jak masz chęci to zrób

13 lut 20:26
bezendu: Nie mam ochoty na prawdo. bo te zadania juz robiłem ja chcę planimetrię przystawanie i
podobieństwo
13 lut 20:28
Trivial: bezendu, nuudy.

13 lut 20:28
bezendu: Trivial może nudy ale ja mam problem z dowodami z planimetrii i dlatego chcę to ćwiczyć.
13 lut 20:32
th: W równoległoboku ABCD dane są: |AB|=18, |BC|=10, ∡ABC=120 stopni.
Punkt K leży na boku AB i |AK|=12. Punkt L jest środkiem boku BC. Proste CK i DL przecinają się
w punkcie M. Oblicz pole czworokąta KBLM.
13 lut 20:41
bezendu:
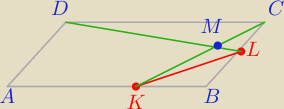
Wyliczyłem KL=
√91
a dalej nie wiem ?
13 lut 20:52
th: Przedłuż bok AB i DL
13 lut 20:56
Mila:
Podobieństwo.
Zadanie1.
W Δ równoramiennymABC są dane: |AC|=|BC|=26 cm, AB|=20 cm. Oblicz odległośćśrodka S wysokości
CD od ramienia AC.
Zadanie 2.
Wykaż, że w trójkącie prostokątnym kwadrat długości przyprostokątnej jest równy iloczynowi
długości przeciwprostokątnej przez długość rzutu prostokątnego tej przyprostokątnej na
przeciwprostokątną.
13 lut 21:02
bezendu:
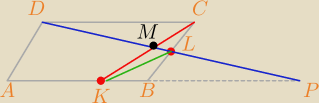
Przedłużyłem...
13 lut 21:03
th: Poszukaj trójkątów podobnych i przystających.
13 lut 21:06
bezendu:
ΔKBL∼ΔKBC
ΔDMC≡ΔPLB
13 lut 21:13
th: ΔDLC≡ΔBLP
ΔKMP~ΔDMC
Pole tego czworokąta to różnica między polem trójkąta KMP a polem trójkąta BLP
13 lut 21:17
th: Wysokość trójkąta KMP wyliczysz z podobieństwa.
13 lut 21:18
bezendu:
W zadaniu pierwszym 21:02
13 lut 21:19
bezendu: A czemu te trójkąty które ja zapisałem nie są poprawne ?
13 lut 21:20
th: Odcinki odpowiednich bokow nie sa proporcjonalne wiec nie sa podobne.
13 lut 21:26
th: A tamte nie sa przystajace bo maja inne katy.Tylko jeden maja wspolny.
13 lut 21:27
bezendu: A zobacz odpowiedź do zadania 21:02 ?
13 lut 21:28
th: dobrze
13 lut 21:30
bezendu:
W drugim nie wiem o co chodzi z tym rzutem ?
13 lut 21:32
th: A to moje zrobiles
13 lut 21:42
Mila:
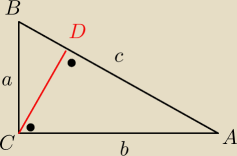
1) dobra odp.
Do zadania 21:02
Masz wykazać, że :
a
2=c*|BD|
b
2=c*|AD|
13 lut 21:43
bezendu:
ΔCDB∼ΔABC
Próbowałem coś
ale nic to nie daje
13 lut 21:58
Mila:
Wybierz dwa boki ΔCDB i...
13 lut 22:01
13 lut 22:03
Mila:
a:BD=bo interesuje Cię przyprostokątna a i jej rzut BD na przeciwprostokątną
=c: a
Przeciwprostokątnej odpowiada przeciwprostokątne w podobnym Δ,
BD leży naprzeciw kąta o mierze α w ΔCDB, a naprzeciw kąta α w ΔABC leży a.
a
2=c*|BD|
13 lut 22:24
13 lut 22:31
Mila:
Popraw. 22:31, patrz na odpowiedniość boków.
13 lut 22:38
13 lut 22:41
Mila:
⇔b2=c*|AD|
cnw
13 lut 22:45
bezendu:
Proszę kolejne zadania.
13 lut 22:46
Mila:
Podobieństwo.
zadanie 3.
W trójkącie prostokątnym jedna z przyprostkątnych jest dwa razy dłuższa od drugiej
przyprostokatnej. Wysokość poprowadzona z wierzchołka kąta prostego dzieli przeciwprostkątną
na dwa odcinki.
Oblicz stosunek długości tych odcinków.
13 lut 22:55
bezendu:
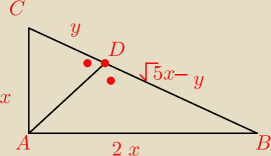
|CB|
2=x
2+(2x)
2
|CB|
2=x
2+4x
2
|CB|=
√5x
może być ta proporcja ?
13 lut 23:05
Ajtek:
Cześć
bezendu 
.
Zaprosiłeś to wpadłem. Jakieś zadanko chcesz?
13 lut 23:26
bezendu: Na razie to to muszę zrobić.
13 lut 23:27
Mila:
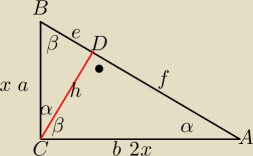
ΔCDB∼ΔCDA⇒
| e | | h | |
| = |
| ⇔h2=e*f ZAPAMIĘTAJ |
| h | | f | |
(2e)
2=e*f
4e
2=e*f
4e=f
13 lut 23:28
bezendu:
A no jest taka własność. Teraz mam kilka obliczeniowych.
13 lut 23:31
Mila:
To dobranoc.

13 lut 23:31
bezendu: Długa droga jeszcze.. Dziękuję i dobranoc

13 lut 23:34
Eta:
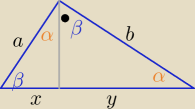
13 lut 23:52
bezendu:
Eta pomożesz w kilku zadaniach może prostych nawet ale muszę ogarnąć.?
13 lut 23:53
Ajtek:
Eta tej własności nie pamiętam, udowodnię ją sobie jutro (tzn. spróbuję)

13 lut 23:53
Eta:

13 lut 23:55
bezendu:
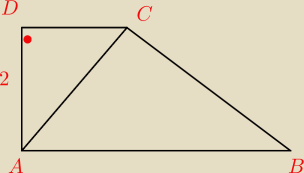
Wiem, że do przedszkolaka ale cóż ja chcę się nauczyć.
Krótsza przekątna trapezu prostokątnego dzieli trapez na dwa trójkąty, z których jeden jest
równoboczny. Znajdź pole tego trapezu wiedząc, że ramię prostopadłe do podstaw ma długość 2.
Jak prosta AC podzieliła kąt prosty przy wierzchołku A ?
13 lut 23:58
Eta:

Czy ten rys. wystarczy?
14 lut 00:02
Eta:
W ... wkleiło się niepotrzebnie

14 lut 00:02
bezendu:
Też mi się tak wydawało ale wolę zapytać eksperta.
14 lut 00:03
Eta:

14 lut 00:04
bezendu:

Ramiona trapezu prostokątnego mają długości 6 i 10. Odcinek łączący środki ramion ma długość
10. Oblicz długości podstaw trapezu.
a+a=20−8
2a=12
a=6
b=14
14 lut 00:08
bezendu: ?
14 lut 00:19
bezendu: ?
14 lut 00:29
Eta:
Dobrzeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeeee

14 lut 00:31
bezendu: Dziękuję jutro wstaję od 6 i liczę zadania.
14 lut 00:36
14 lut 00:38
Ajtek:
bezendu, wyśpij się. Wypoczęty umysł jest Twoim najlepszym kumplem

.
14 lut 00:39

 ale jak masz chęci to zrób
ale jak masz chęci to zrób 

 Wyliczyłem KL=√91
a dalej nie wiem ?
Wyliczyłem KL=√91
a dalej nie wiem ?
 Przedłużyłem...
Przedłużyłem...
 1) dobra odp.
Do zadania 21:02
Masz wykazać, że :
a2=c*|BD|
b2=c*|AD|
1) dobra odp.
Do zadania 21:02
Masz wykazać, że :
a2=c*|BD|
b2=c*|AD|
 |CB|2=x2+(2x)2
|CB|2=x2+4x2
|CB|=√5x
|CB|2=x2+(2x)2
|CB|2=x2+4x2
|CB|=√5x
 .
Zaprosiłeś to wpadłem. Jakieś zadanko chcesz?
.
Zaprosiłeś to wpadłem. Jakieś zadanko chcesz?
 ΔCDB∼ΔCDA⇒
ΔCDB∼ΔCDA⇒





 Wiem, że do przedszkolaka ale cóż ja chcę się nauczyć.
Krótsza przekątna trapezu prostokątnego dzieli trapez na dwa trójkąty, z których jeden jest
równoboczny. Znajdź pole tego trapezu wiedząc, że ramię prostopadłe do podstaw ma długość 2.
Jak prosta AC podzieliła kąt prosty przy wierzchołku A ?
Wiem, że do przedszkolaka ale cóż ja chcę się nauczyć.
Krótsza przekątna trapezu prostokątnego dzieli trapez na dwa trójkąty, z których jeden jest
równoboczny. Znajdź pole tego trapezu wiedząc, że ramię prostopadłe do podstaw ma długość 2.
Jak prosta AC podzieliła kąt prosty przy wierzchołku A ?
 Czy ten rys. wystarczy?
Czy ten rys. wystarczy?


 Ramiona trapezu prostokątnego mają długości 6 i 10. Odcinek łączący środki ramion ma długość
10. Oblicz długości podstaw trapezu.
a+a=20−8
2a=12
a=6
b=14
Ramiona trapezu prostokątnego mają długości 6 i 10. Odcinek łączący środki ramion ma długość
10. Oblicz długości podstaw trapezu.
a+a=20−8
2a=12
a=6
b=14

 na dobranoc
na dobranoc 

 .
.