okrąg i prosta :) Blue: Znajdź te wartości parametru m , dla których prosta y=x+m ma dwa punkty wspólne z okręgiem x²+y² = 2. Ja to rozwiązałam tak na logikę, bo skoro ten okrąg ma środek w punkcie (0,0), to wiadomo,że przecina oś OY w punktach (0,√2) i (0,−√2) . Wiadomo te, żeprosta y=x+m przecina oś OY w punkcie (0,m) w takim razie m jest zawarte w (−√2,√2)... A w odpowiedziach mam (−2,2). Co ja tutaj źle rozumuję? HELP!

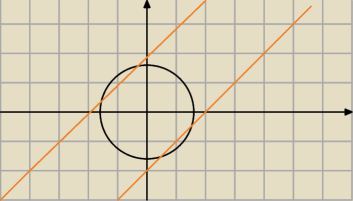
wredulus_pospolitus: dobry tok rozumowania ... ale niestety ... nie wszystkie proste ujęłaś ... (np te narysowane)

wredulus_pospolitus: musisz sprawdzić dla jakiego 'm' prosta dana równaniem y=x+m będzie STYCZNA do okręgu (1 punkt wspólny) ... i stąd będzie (−2,2)

J: Musisz zbadać,kiedy ( dla jekego m ) układ równań: prosta i okrąg ma 2 rozwiązania.

J: x² + (x+m)² − 2 = 0 ⇔ x² + x² +2mx +m² − 2 = 0 ⇔2x² +2mx + m² − 2 = 0 Warunek: Δ > 0 Δ = 4m² − 8(m² −2) = 4m² − 8m² +16 = − 4m² + 16 − 4m² + 16 > 0 ⇔ 4m² < 16 ⇔ m² < 4 ⇔ m ∊ (−2,2)

pw: okrąg o środku A(0,0) i promieniu 2=√2 będzie miał 2 punkty wspólne z prostą y=x+m jeśli ta prosta będzie w odległości mniejszej od środka okręgu niż r=√2 Oznaczenia: A środek okręgu (0,0) B punkt na prostej (x,y) ⇒ (x,x+m) bo y=x+m d|AB|<√2 zatem (0−x)² + (0−y)²<2 x²+y²<2 x²+(x+m)²<2 x²+x²+2mx+m²−2<0 2x²+2mx+m²−2<0 kiedy ta nierówność będzie <0, gdy Δ>0 zatem Δ=(2m)²−4*2*(m²−2)=4m²−8m²+16=16−4m² Δ>0 16−4m²>0 m²−4<0 m∊(−2;2)

Blue: ok, rozumiem, dzięki