styczna w punkcie, pochodna w pkt równa nieskończonosc Adrian: witam, nie wiem jak interpretować wynik pochodnej w pkt nieskończoność. liczę równanie stycznej do funkcji √x+1 w pkt x=−1 równanie po podstawieniu do wzoru wygląda tak y= ∞(x+1) wiadomo że tą styczna to x=−1 ale jak to w innym przypadku gdy nie da się wykresu narysowac

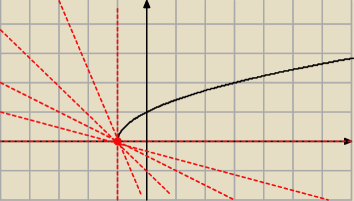
wredulus_pospolitus: drogi studencie nim się zacznie robić zadanie ... warto pomyśleć chwilkę 1) jaka jest dziedzina funkcji f(x) 2) a możesz narysować f(x) 3) spróbuj narysować styczną do f(x) w punkcie x=−1 4) a może sie uda jakąś inną styczną i jeszcze inną ... i jeszcze inną jak widzisz ... w punkcie x=−1 jest NIESKOŃCZENIE wiele stycznych do wykresu f(x) teraz zastanów się dlaczego

PW: Z lewej strony punktu x₀ = −1 dziedziny już nie ma, więc o stycznej nie bardzo można mówić w klasycznym sensie. Po drugie (ważniejsze) pochodna (jednostronna) w punkcie x₀ = −1 nie istnieje. Po prostu −1 nie należy do dziedziny pochodnej. Koniec.

PW: A, szacunek, nie odświeżałem przez jakiś czas, więc odpowiedzi wredulusa pospolitusa nie widziałem.