Liczby zespolone Dżej: Cześć, mam takie zadanie, czy dobrze je rozwiązuję? z³=(i−√3)¹⁵ |z|= √1²+√−3²=2 φ= cos ¹₂= ^π₃ i sin= ^√−3₂=−^π₃ z=|z|ⁿ(cos^φ+2kπ_n+isin^φ+2kπ_n)¹⁵ k= 0,1 k=0 z=8(cos^π₃+2*0*π₂−isin^π₃+2*0*π₂)¹⁵=8(cos^5π₂−isin^5π₂) k=1 z=8(cos^π₃+2*1*π₂−isin^π₃+2*1*π₂)¹⁵=8(cos^15π₂−isin^15π₂)

PW:

	1		π		√−3		π
φ= cos		=		i sin=		=−
	2		3		2		3

to błędy (wiesz o co idzie, ale zapisujesz źle).

Dżej: Mam tam minusa przy i sin= − ^π₃. Druga część zadania to otrzymane pierwiastki zaznaczyć na płaszczyźnie zespolonej. Czy naeżą do zbioru: A={z∊ℂ :z≤ |3i+z−1| ≤3 ∧ Argz∊<0,π>} Czy przy |3i+z−1| mam podstawić (i−√3)¹⁵, czy może |z|? Argz jest to ^π₃?

Dżej: Ktoś może coś podpowiedzieć?

Dżej: jeżeli Argz= ^π₃ to zawiera się w przedziale <0,π> ale nie wiem co zrobić z przedziałem 2≤|3i+z−1|≤3 Ma może ktoś jakąś podpowiedź?

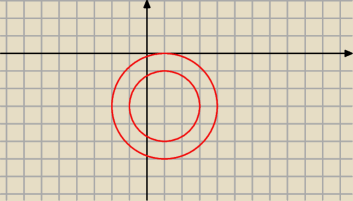
MQ: Warunek 2≤|3i+z−1|≤3 oznacza, że z mieści się w pierścieniu między okręgami o środku w p. 1−3i i promieniach 2 i 3.

Dżej: Aaa, dzięki za wyjaśnienie.