dziedzina dunkcji f
Draco: wyznacz dziedzinę funkcji f..
f(x)=√log(1+x)−log(8−x)
wytłumaczy ktoś?
13 lut 11:17
J: Warunki:
1) (1+x) > 0
2) (8−x) > 0
3) log(1+x) − log(8−x) ≥ 0
13 lut 11:19
5-latek: 1+x>0 i 8−x>0 i log(1+x)−log(8−x)≥0
13 lut 11:19
5-latek: Czesc

13 lut 11:20
J: Hej

13 lut 11:20
Draco: | | 1+x | |
dobra więc teraz log |
| ≥0 |
| | 8−x | |
i liczyć osobno dla niej dziedzine czy tylko rozwiązać tą nierówność?
13 lut 11:30
J: Tylko rozwiązać, bo założenia już masz zrobione.
13 lut 11:35
Draco: czy zrobić tak że przenieść i żeby było:
log(1+x)≥log(8−x)
1+x≥8−x
więc rozwiązanie będzie takie:
| | 7 | |
dziedzina funkcji to x∊R / {−1, |
| , 8} |
| | 2 | |
dobrze?
13 lut 11:36
J: Teraz masz trzy warunki:
1) x > −1
2) x < 8
| | 7 | |
3) x ≥ |
| i szukasz części wspólnej tych trzech zbiorów. |
| | 2 | |
13 lut 11:44
Draco: czyli będzie to D: (x∊R: 7/2, x, 8)
dobrze

13 lut 11:54
J:
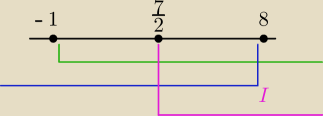
I gdzie jest część wspólna ?
13 lut 11:58
pw: założenia:
1+x>0 8−x>0
x>−1 x<8
mamy pierwszy przedział x∊(−1;8)
teraz
log(1+x)−log(8−x)≥0
log(1+x)≥log(8−x)
1+x≥8−x
2x≥7
x≥3,5
zatem dziedzina to;
x∊[3,5 ; 8)
13 lut 11:59
5-latek:
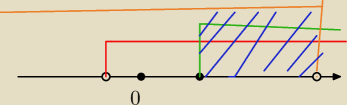
13 lut 12:04
Mati:
13 lut 12:05



 I gdzie jest część wspólna ?
I gdzie jest część wspólna ?
