Punkty przegięcia i przedzialy wypuklosci/wkleslosci f(x)=e^1/x xxx: Wyznaczyć punkty przegięcia i przedziały wypuklosci i wkleslosci f(x)=e ¹/x (to jest e do potegi 1przez x) PP wyszedl mi −1/2 (ale nie wiem czy dobrze? ) a przedzialy wkleslosci (−1/2;+∞) i wypuklosci(−∞;−1/2) Generalnie mam z tym problem...

wredulus_pospolitus: punkt przegięcia dobrze wyznaczony ... ale przedziały źle −−−− patrz dziedzina funkcji

J: Nie łapię. f(x) = e^1/x

	1		1
f'(x) = e1/x*(−		) i f'(x) = 0 dla x = −		?
	x2		2

J: Witaj "wredulus" Oświeć mnie

xxx: czyli moimi przedzialami beda wypuklosc(−∞;−1/2) I Wkleslosc(−1/2;0) i (0;+∞) ?

wredulus_pospolitus: J ... toć 0 nie należy do dziedziny

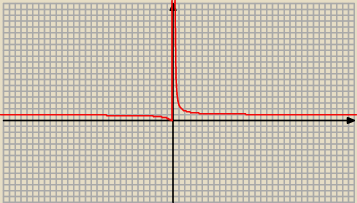
Janek191: Będzie taki wykres Nie ma punktu przegięcia . f' ( x) < 0 − funkcja maleje w swojej dziedzinie ( − ∞ . 0 ) − wklęsła ; ( 0; + ∞ ) − wypukła

J: Muszę poćwiczyć wyznaczanie dziedziny funkcji

J:

	1
Nie załapałem,dlaczego punkt przegięcia miałby być w punkcie x = −		, skoro pierwsza
	2

pochodna nigdy się nie zeruje. Stąd było moje pytanie,dlaczego pierwsza pochodna ma być

	1
równa zero dla x = −		?
	2