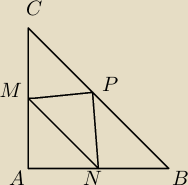
pomocy Martaaa: W trójkąt prostokątny równoramienny ABC (|∡BAC| = 90◯) wpisujemy trójkąt MNP tak, że P jest środkiem boku BC, a M ∊ AC, N ∊ AB oraz MN ∥ BC (jak na rysunku). Jak należy wybrać punkty M i N, aby pole trójkąta MNP było największe, jeśli |AB| = |AC| = 4 cm?

Aga1.: Czy to zadanie jest z liceum?

Martaaa: tak

Martaaa: Doszłam do tego, że |BC| = 4 √2 Więc |BP| = |CP| = 2 √2 i utknęłam

Aga1.: Obliczyłam pole trójkąta ABC i ANP i NBP oraz MPC. i zapisałam pole trójkąta NMP jako różnicę odpowiednich pól.(∡B=∡C=45⁰) W moich obliczeniach pojawiają się dwie niewiadome i mam funkcję dwóch zmiennych.Pewnie nie dostrzegam jakiejś zależności .

J: Myslę,że mozna spróbować tak: PΔ(MNP) = PΔ(ABC) − PΔ(MNA) − 2PΔ(PNB) Niech x = IAMI = IANI, wtedy PΔ(MNA) = 0.5x² INBI = ( 4 − x) i PΔ(NBP) = 0.5*(4 − x)*2 Mamy: PΔ(MNP) = 0.5*4² − 0.5*x² − 2*0.5*(4−x)*2

Martaaa: Dzięki za wskazówkę Aga. Rozwiązałam