geometria romek: Ramiona trapezu podzielono na trzy równe części prostymi równoległymi do podstaw. Otrzymano w ten sposób trzy nowe trapezy. Pola skrajnych trapezów wynoszą S1 i S2. Oblicz pole środkowego trapezu.

wredulus_pospolitus: wskazówka: znajdź zależność pomiędzy podstawami kolejnych trapezików

romek: a może coś więcej?

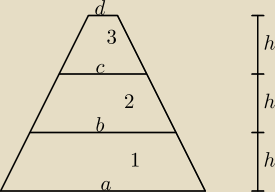
wredulus_pospolitus: albo jak wolisz:

	a+d
P1+2+3 =		*(3h)
	2

	a+b		c+d		a+b+c+d		a+d		b+c
P1 +P3 =		*h +		*h =		*h =		*h +		*h
	2		2		2		2		2

	b+c
P2 =		*h
	2

i co dalej można zrobić

romek: do tego to akurat dzoszedłem sam. nie wiem co mam zrobic dalej

Aga1.: P₁+P₃=S₁+S₂ Wykorzystaj wzór na środkową w trapezie.

	a+c		b+d
b=		, c=		i podstaw do P2
	2		2

Domel: Szukane S₃

	a+b		c+d		a+d		b+c
S1 =		h ; S2 =		h ; S =		3h : S3 =		h
	2		2		2		2

S₃ = S − S₁ − S₂

	c+d		a+b		c+d
S3 =		3h −		h −		h
	2		2		2

	1
S3 =		h*[3(a+d) − (a+b) − (c+d)]
	2

	1
S3 =		h*(3a + 3d − a − b − c − d)
	2

	1
S3 =		h*(2a − b − c + 2d)
	2

	a+d		b+c
S3 =		2h −		h
	2		2

	2
S3 =		S − S3
	3

	2
2*S3 =		S
	3

	1
S3 =		S
	3

	1
S3 =		*(S1 + S2 + S3)
	3

	1		1
S3 −		S3 =		*(S1 + S2)
	3		3

2		1
	S3 =		*(S1 + S2)
3		3

	1
S3 =		*(S1 + S2)
	2