planimetria bla bla: Dany jest trójkąt prostokątny ABC o przyprostokątnycj AC, BC. Odcinek CD jest wysokością trójkąta, ∡CAB=α a punkt O jest środkiem okręgu opisanego na trójkącie. Wyznacz miarę konta DCO.

bla bla:

AROB: pomagam

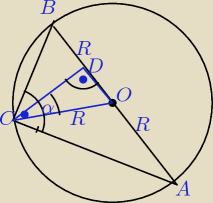
AROB: Dane: AC, BC α = ? AB = √AC² + BC², AB = 2R

	√AC2 + BC2
więc R =
	2

	CD		BC
ΔADC ∼ ΔABC, stąd		=
	AC		AB

Z proporcji tej wyznaczamy CD :

	AC * BC		AC * BC
CD =		=
	AB		√AC2 + BC2

	CD
		= cosα
	R

	AC * BC   2R		AC * BC		AC * BC
cosα =		=		=		=
	R		2R2		AC2 + BC2   2 *   4

	2 * AC * BC
=
	AC2 + BC2

bla bla: nie za bardzo rozumiem skąd wzieło się że ΔADC jest podobny do ABC...

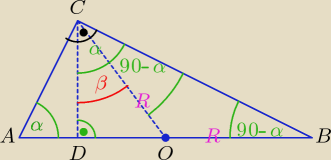
Bogdan: Dobry wieczór. β = α − (90 − α) = 2α − 90

AROB: bla bla, Trójkąty ADC i ABC są podobne, bo są trójkątami prostokątnymi, które mają wspólny kąt ostry CAD. Ale ciekawsze rozwiązanie podał Bogdan, więc skorzystaj z niego. Dobry wieczór, Bogdanie i Eto

Bogdan: Witaj [PAROB]]

Bogdan: Przepraszam, jeszcze raz. Witaj AROB

bla bla: acha, już wiem o co chodzi Dziekuje AROBie i Bogdanie