W trójkącie ABC dane są : |AC|=6, |BC|=4, |kąt ACB|=120^o. Wyznacz długość odcin
aS :): W trójkącie ABC dane są : |AC|=6, |BC|=4, |kąt ACB|=120
o. Wyznacz długość odcinków , na jakie
został podzielony najdłuższy bok przez dwusieczną przeciwległego kąta. Wyznacz długość
fragmentu dwusiecznej danego kąta zawartej w opisanym trójkącie.
Z twierdzienia cos obliczyłem sobie bok |AB|= 2
√19, a teraz nie wiem co dalej
Z góry dziękuję za pomoc
pigor: ..., no to dalej , niech D punkt podziału boku AB przez dwusieczną
CD i dla uproszczenia zapisu
|AD|=x=? ⇒
|BD|=2√19−x=? i
|CD|=d=?,
| | x | | 2√19−x | |
to z tw. o dwusiecznej np. |
| = |
| ⇔ 2x= 6√19−3x ⇔ |
| | 6 | | 4 | |
⇔ 5x= 6
√19 ⇔ x=
|AD|=1,2√19 , oraz
|BD|=0,8√19, no to teraz jeśli
np. |∡CAD|=α, znowu z tw, cosinusów w .ΔABC :
| | 62+(2√19)2−42 | | 20+4*19 | | 5+19 | | 4 | |
cosα= |
| = |
| = |
| = |
| ⇒ |
| | 2*6*2√19 | | 24√19 | | 6√19 | | √19 | |
| | 16 | | 3 | | √3 | |
⇒ sin2α=1− |
| = |
| ⇒ sinα= |
| , więc z tw. sinusów w ΔACD : |
| | 19 | | 19 | | √19 | |
| d | | x | | 2xsinα | | 2*1,2√19√3 | |
| = |
| ⇔ d= |
| , czyli d= |
| ⇒ |
| sinα | | sin60o | | √3 | | √19*√3 | |
⇒ d=
|CD|= 2,4 − szukana
długość odcinka dwusiecznej. ...
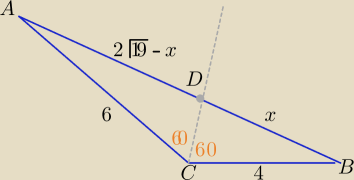x< 2√19
Z tw. kosinusów |AB|= 2√19