Monotoniczność i ekstrema Kacper: Hej, policzyłem dwa zadania z monotonicznością i ekstremami, czy ktoś mógłby mi powiedzieć czy dobrze rozwiązałem. Pierwsze: f(x) = ^x2₂ − ln(x) Wynik: Df : x ∊ (0, +∞) f(x)↗dla x ∊ (1,+∞), f(x)↘dla x ∊ (0,1) Funkcja osiąga minimum lokalne w punkcie (1,¹₂) Drugie: f(x) = ^x2₂ − ¹_x Wynik: Df : x ∊ ℛ\{0} f(x)↗dla x ∊ (1,+∞), f(x)↘dla x ∊ (−∞,0)∪(0,1) Funkcja osiąga minimum lokalne w punkcie (1,1¹₂) Byłbym bardzo wdzięczny za sprawdzenie, z góry dziękuję.

Kacper: bump.pls

Kacper: bump.pls

Krzysiek: drugie źle

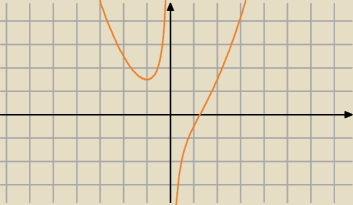
Aga1.: Tak wygląda wykres funkcji