fu
Radek:
Wyznacz te wartości parametru m , dla których równanie
mx2+(m−3)x − m + 2 = 0 ma co najmniej jedno dodatnie rozwiązanie.
dla m=0
jedno rozwiązanie a dalej jak to analizować ?
12 lut 16:14
Piotr 10: Ja bym proponował zrobić zdarzenie przeciwne, tak chyba łatwiej, pomyśl nad tym
12 lut 16:14
Radek: ok
12 lut 16:16
Radek:
Jednak nie wpadłem na to.

12 lut 17:39
Mila:
1) m=0, to masz równanie :
| | 2 | |
−3x=−2 ma jedno rozwiązanie, x= |
| >0 |
| | 3 | |
2) m≠0 masz równanie kwadratowe, równanie to ma co najmniej jedno rozwiązanie , gdy:
Δ≥0
Dalej wiesz?
12 lut 18:12
Radek:
Ale tylko Δ≥0 wystarczy ?
12 lut 18:15
ZKS:
Nie. Sposób który zaproponował Piotr 10 jest bardzo dobry. Teraz należy tylko dać
założenia kiedy mamy dwa pierwiastki ujemne. Należy ten zbiór wyrzucić ze zbioru
jaki otrzymamy z Δ ≥ 0.
12 lut 18:20
Radek: I znowu nie wiem o co chodzi..
12 lut 18:21
ZKS:
Oczywiście nie ujemne tylko niedodatnie bo w treści mamy dodatnie czyli x = 0 też nie spełnia.
12 lut 18:24
ZKS:
Podaj warunki na to aby pierwiastki były niedodatnie.
12 lut 18:24
Radek: niedodatnie
x1+x2≤0
x1x2≥0
12 lut 18:27
Domel: No i dalej to wzorki Pana V
12 lut 18:29
ZKS:
To rozwiązuj nierówności i zapisz co otrzymasz.
12 lut 18:31
Radek:
Musi być założenie, że m≠0 mianownik ?
−m(m−2)≥0
12 lut 18:33
ZKS:
Jasne że musi być.
12 lut 18:35
Radek: z pierwszego warunku
(0,2>
12 lut 18:36
ZKS:
Napisałeś go jako drugi warunek.

Ale rozwiązanie nierówności

.
12 lut 18:42
12 lut 18:45
ZKS:
Chyba zapomniałeś czegoś uwzględnić.

Ten minus się na Ciebie obraził że go olałeś.
12 lut 18:47
Radek:
m(−m+3)≤0
−m(m−3)≤0
m∊(−∞,0)suma<3,∞)
12 lut 18:50
ZKS:

.
12 lut 18:51
ZKS:
Czyli kiedy otrzymasz pierwiastki niedodatnie?
12 lut 18:51
Radek: część wspólna ?
12 lut 18:53
ZKS:
Yo.
12 lut 18:55
Radek: m=3
12 lut 18:56
ZKS:
Serio?
12 lut 19:00
Radek: To jak ?
12 lut 19:00
ZKS:
Narysuj sobie te zbiory jeżeli od razu nie widzisz części wspólnej.
12 lut 19:01
Radek:
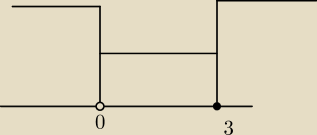
12 lut 19:08
ZKS:
No gdzie spójrz na swoje zbiory jakie masz. Napisz je.
12 lut 19:11
Radek: 3 tylko spełnia
12 lut 19:15
ZKS:
Radek napisz swoje zbiory jakie otrzymałeś z tych nierówności.
12 lut 19:18
Radek: m∊(0,3>
m∊(−∞,0)suma<3,∞)
12 lut 19:19
ZKS:
Czy dla Ciebie m ∊ (0 ; 2] to to samo co m ∊ (0 ; 3]?
12 lut 19:20
Radek:
Brak części wspólnej
12 lut 19:25
ZKS:

. Czyli jaką dasz końcową odpowiedź do tego zadania.
12 lut 19:29
Radek: Posiada tylko jeden pierwiastek dodatni
12 lut 19:30
ZKS:
Jaki przedział podasz skoro to co Ci wyszło czyli brak części wspólnej miałeś wyrzucić
z przedziału z warunku Δ ≥ 0? Oczywiście pamiętaj co dostałeś dla m = 0.
12 lut 19:32
Radek: nie rozumiem co napisałeś ?
12 lut 19:34
ZKS:
Masz podać przedział dla jakiego m równanie ma co najmniej jedno dodatnie rozwiązanie.
Wcześniej napisałem że należy zbiór (dla których mamy rozwiązania niedodatnie wyrzucić)
nazwijmy go A ze zbioru jaki otrzymamy z Δ ≥ 0 nazwijmy go B.
Teraz masz zrobić B \ A i podać zbiór.
12 lut 19:38
Radek: a ok

12 lut 19:38
ZKS:
Szybko szybko bo mi się śpieszy.

A chcę sprawdzić czy dobrą podasz odpowiedź.
12 lut 19:39
12 lut 19:43
ZKS:
A m = 0 uwzględniamy czy nie?
12 lut 19:43
Radek: tak
12 lut 19:45
ZKS:
Wszystko

.
12 lut 19:46
Domel: No dobra − może to ojaśni
Badam (wg koncepcji Piotra 10) zdarzenie przeciwne
| | b | | m−3 | |
1. − |
| ≤ 0 => − |
| ≤ 0 |
| | a | | m | |
ad. 1
a)
| ⎧ | −(m−3) ≤ 0 => −m+3 ≤ 0 => m ≥ 3 | |
| ⎩ | m > 0 |
|
więc z układu 1a) wynika m ≥ 3
b)
| ⎧ | −(m−3) ≥ 0 => −m+3 ≥ 0 => m ≤ 3 | |
| ⎩ | m < 0 |
|
więc z układu 1b) wynika m < 0
m=0 nie należy do dziedziny
Z 1a) i 1b) wynika, że m∊(−
∞;0) ∪ <3;+
∞)
ad 2.
a)
| ⎧ | −m+2 ≤ 0 => m ≥ 2 | |
| ⎩ | m < 0 |
|
więc układ 2a) wynika m ≥ 3
b)
| ⎧ | −m+2 ≥ 0 => m ≤ 2 | |
| ⎩ | m > 0 |
|
więc z układu 2b) wynika, że m∊(0;2>
Z 2a) i 2b) wynika, że m∊(0;2>
Równania 1 i 2 nie posiadają wspólnego przedziału więc biorąc pod uwagę zdarzenie przeciwne dla
każdego m oprócz m=0 (∉D) równanie będzie posiadało co najmniej 1 dodatnie rozwiązania
12 lut 19:47
Domel: Sorki
tak to jest jak się kopiuje

powinno być:
więc układ 2a) jest sprzeczny
dalej chyba dobrze
12 lut 19:50

 Ale rozwiązanie nierówności
Ale rozwiązanie nierówności  .
.
 Ten minus się na Ciebie obraził że go olałeś.
Ten minus się na Ciebie obraził że go olałeś.
 .
.

 . Czyli jaką dasz końcową odpowiedź do tego zadania.
. Czyli jaką dasz końcową odpowiedź do tego zadania.

 A chcę sprawdzić czy dobrą podasz odpowiedź.
A chcę sprawdzić czy dobrą podasz odpowiedź.
 .
.
 powinno być:
więc układ 2a) jest sprzeczny
dalej chyba dobrze
powinno być:
więc układ 2a) jest sprzeczny
dalej chyba dobrze