Ciągi i trygonometria maramasike: 1. Wyznacz ciąg arytmetyczny, w którym suma czwartego i ósmego wyrazu wynosi −7/3, a iloczyn drugiego i trzeciego wyrazu jest równy −1/36. 2. Suma pierwszego i dziesiątego wyrazu ciągu arytmetycznego jest równa 34, a różnica ósmego i trzeciego wyrazu wynosi 5{2}. Wyznacz wzór ogólny tego ciągu. 3. Dany jest ciąg arytmetyczny (an). Wyznacz równanie prostej, do której należą punkty o współrzędnych (n, an), jeśli wiadomo, że: a) a1=7, r=0 b) a1=5, r=−3. 4. Zbuduj kąt α, 0 stopni<α<90 stopni, wiedząc, że: a) sinα=2/3 b)cosα=4/5 c)tgα=3 d)ctgα=2.

J: Zad 1)

	7		7
a4 + a8 = −		⇔ a1 +3r + a1 + 7r = −
	3		3

	1		1
a2 * a3 = −		⇔ (a1 + r)(a1 + 2r) = −
	36		36

Układ równań o dwóch niewiadomych; a₁ i r

Janek191: Np. 1 Korzystamy z wzoru a_n = a₁ + ( n − 1)*r więc mamy

	−7		− 7
a4 + a8 =		⇒ (a1 + 3r) + ( a1 + 7r) =		/ * 3
	3		3

	−1		−1
a2*a3 =		⇒ ( a1 + r)*( a1 + 2r) =		/ *36
	36		36

	7
6 a1 + 30 r = − 7 ⇒ 6 a1 = − 30 r − 7 ⇒ a1 = − 5r −
	6

36*(a₁² + 2a₁ r + a₁ r + 2 r² )= − 1

	7
a1 = − 5r −
	6

36*( a₁² + 3a₁ r + 2 r²) = − 1 itd.

J: Myśle "Janek191",że ... daremny trud

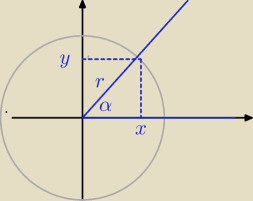
Janek191: z.4

	2		y		2
0o < α < 90o i sin α =		⇒		=		⇒ y = 2 i r = 3
	3		r		2

x² + y² = r² ⇒ x² = r² − y² = 3² − 2² = 9 − 4 = 5 ⇒ x = √5

maramasike: dziękuję bardzo prosiłabym jeszcze o jakąś podpowiedź, jak rozwiązać zad. 3

J: a) Jeżeli a₁ = 7 i r = 0,to jest to ciąg stały.Wszystkie jego wyrazy są równe 7 i należą do prostej o równaniu y = 7

J: b) wyznacz 2 wyrazy tego ciągu i napisz równanie prostej przechodzącej przez punkty A(1,a₁) i B(2,a₂)