trapez
iza: Dłuższe ramię trapezu ma długość 6√2, natomiast krótsza przekątna dzieli go na dwa trójkąty
prostokątne równoramienne . oblicz pole trapezu i długość drugiej przekątnej
12 lut 14:12
Janek191:
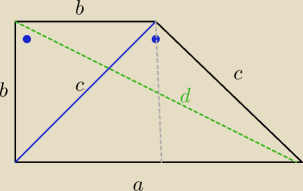
Mamy
c
2 + c
2 = a
2
2 c
2 = ( 6
√2)
2 = 72
c
2 = 36
c = 6
−−−−−−−
| | 6 | |
c = b √2 ⇒ 6 = b √2 ⇒ b = |
| = 3√2 |
| | √2 | |
b = 3
√2
−−−−−−−
Pole P
P = 0,5*( a + b)*b = 0,5*( 6
√2 + 3
√2)*3
√2 = 0,5*9p{2]*3
√2 = 27 [ j
2 ]
============================================
oraz
d
2 = a
2 + b
2 = 72 + 18 = 90 = 9*10
d = 3
√10
==========
12 lut 14:28
J:
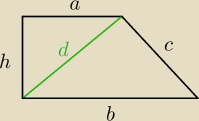
c = 6
√2
b = c*
√2
d = c
h = a i a
2 + a
2 = d
2 = c
2
12 lut 14:28
J: Janek... c jest podane w treści zadania
( dłuższe ramię)
12 lut 14:30
iza: J czemu b= c*√2 a nie b=6√2+6√2?
12 lut 14:44
J: b to przekątna kwadratu o boku c, czyli b = c
√2 ( c mamy podane c = 6
√2 )
12 lut 14:46
ola: no właśnie c = 6
√2 a nie
√2 
12 lut 14:47
ola: czemu jej tak mieszasz?
12 lut 14:47
Janek191:
Ale zawaliłem
Zrobiłem inne zadanie − sorry !
12 lut 14:48
J: Zauważ, że podstawa trapezu "b" ( której nie znamy) jest przekatną kwadratu o boku c (bo c=d).
12 lut 14:50
iza: no tak
12 lut 14:52
iza: a jak obliczyć drugą przekatną?
12 lut 15:02
iza: już wiem z Pitagorasa
12 lut 15:03
J: Tw Pitagorasa, masz b i h.
12 lut 15:03