nierownosci z parametrem
bolik: Rozwiąż nierówność (4−m)x22−3x+m+4>0 dla x∊R
11 lut 22:50
Ajtek:
1o
4−m>0 → ramiona paraboli w górę.
2o
Δ<0 wykres funkcji ponad osią Ox.
Rozwiązaniem jest część wspólna tych przedziałów.
11 lut 22:52
ZKS:
Jeżeli autor tematu się nie pomylił to należy rozwiązać nierówność.
11 lut 22:55
Ajtek:
A ja się gdzieś machnąłem?
11 lut 22:56
bolik : czy w 1) Δm=320 ?
11 lut 22:59
Ajtek:
Nie wiem, nie liczę. Podpowiadam tylko
.
11 lut 23:00
Ajtek:
W warunku 1o nie musisz liczyć Δ. Zwykła nierówność liniowa do rozwiązania.
11 lut 23:01
bolik: czyli w 1)
bedzie (4−m)x−3x+m+4>0
4x−mx−3x+m+4>0
x−mx+m+4>0
x(1−m)+m+4>4 ?
11 lut 23:03
Ajtek:
Nic nie wymnażaj. Masz do rozwiązania nierówność (warunek), aby ramiona paraboli były
skierowane do góry to a>0. W Twoim przypadku a=4−m, zatem 4−m>0 i tyle.
11 lut 23:06
ZKS:
Jeżeli treść brzmi dla jakich wartości parametrów m ta nierówność jest spełniona dla x ∊ R to
Twoje
Ajtek warunki są
.
11 lut 23:07
bolik: no to wyjdzie mi, że m<4 a co z tym dalej?
11 lut 23:09
Ajtek:
Ufffff i to jest powód do śmiechu
. A ja nadal nie widzę błędu w treści zadania
.
11 lut 23:09
Ajtek:
Świetnie. Masz 1
o warunek z głowy. Teraz zajmujesz się 2
o czyli Δ<0.
Liczysz Δ, gdzie a=(4−m); b=−3; c=(m+4)
Działaj
.
11 lut 23:11
bolik: tresc jest ok,sprawdzałem 2 razy
11 lut 23:11
wredulus_pospolitus:
nie ... treść NIE JEST ok
treść winna brzmieć: dla jakiego parametru 'm' nierówność .... jest spełniona dla x∊R
11 lut 23:13
Ajtek:
Jak ja się nie lubię domyślać treści, tutaj domyśliłem się od razu
.
11 lut 23:14
bolik: Δ= −4m2 − 55
11 lut 23:14
ZKS:
To jest z jakiejś książki zadanie?
11 lut 23:15
bolik: teraz przyrównuje −4m2−55<0
tak?
11 lut 23:16
bolik: nie wiem, bylo podane na lekcji jako zadanie domowe przez nauuczyciela
11 lut 23:17
Ajtek:
Zapisz raz jeszcze przykład. Coś mi się nie podoba:
(4−m)x22−3x+m+4>0
Ta czerwona dwójka.
11 lut 23:17
bolik: pomyłka, przy podstawianiu do kwadratu wcisnęłami sie dwa razy 2
(4−m)x2−3x+m+4>0
11 lut 23:19
ZKS:
Pewnie źle usłyszałeś treść.
11 lut 23:21
Ajtek:
Pokaż jak liczysz Δ.
11 lut 23:22
bolik: Δ= 9−4(4−m)(m+4)
11 lut 23:23
Ajtek:
A fakt. Zapomniałem o 4 ze wzoru
. Tak teraz rozwiązujesz nierówność −4m
2−55<0
11 lut 23:24
bolik: (4−m)(4+m) = 16−m
2
zatem 9−4(16−m
2) = 9−64
+4m
2= 4m
2−55
11 lut 23:25
bolik: jak ta nierownosc rozwiązac?
11 lut 23:28
Ajtek:
Albo klasycznie Δ, albo widzę, że mam niepełne równanie kwadratowe, czyli mogę:
4m
2<55
Wyznaczasz przedział z warunku 2
o. Teraz część wspólna tych przedziałów. Pamiętam o założeniu,
że m<4 z 1
o warunku
11 lut 23:33
bolik: nie widzę części wspólnej... a cos na pewno jest!
11 lut 23:35
bolik: jak to rozkłada się na wspólnej osi?
11 lut 23:35
Ajtek:
Jasne, że ośka. Wiesz więcej niż myślałem
11 lut 23:36
bolik: m∊(− √55/2 , √55/2 ) ?
11 lut 23:39
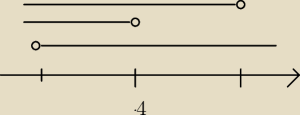
bolik: mogłbyś mi to narysować na jednej wspólnej osi? : D
11 lut 23:40
Ajtek:
Yhy
. Wiesz już o co chodzi
Straszne to jest
11 lut 23:42
bolik:
11 lut 23:43
Ajtek:
A=4
B=
√55/2
C=−
√55/2
Widać
11 lut 23:45
bolik: widzę,widzę!
dzięki!
11 lut 23:48
Ajtek:
Powodzenia, myśl
.
11 lut 23:48