Bardzo proszę o rozwiązanie, mam jutro sprawdzian a nic nie umiem. Karo: Stereometria Zad.1. W graniastosłupie prawidłowym czworokątnym przekątna podstawy równa się d, a kąt nachylenia przekątnej ściany bocznej do krawędzi podstawy wynosi α. a ) Obliczyć objętość graniastosłupa przyjmując : d = 2√2 cm, α = 60 º. b ) Wyznaczyć kąt β, jaki tworzy przekątna podstawy z przekątną ściany bocznej, oraz zbadać jakie wartości może ten kąt przyjmować. Zad.2. Sześcian o krawędzi a = 12 cm rozcięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do płaszczyzny podstawy pod kątem 30 º. Obliczyć pole i obwód otrzymanego przekroju. Zad.3. Obwód podstawy prostopadłościanu wynosi 34, a przekątna bryły ma długość 13√2 i tworzy z podstawą kąt α = 45º. Obliczyć objętość tego prostopadłościanu i pole powierzchni przekroju wyznaczonego przez tę przekątną i dłuższy bok podstawy. Zad.4. W graniastosłupie prawidłowym czworokątnym suma długości jego krawędzi jest równa 48 cm, a pole powierzchni całkowitej 90 cm2. Oblicz długości krawędzi graniastosłupa i jego objętość. Zad.5. Podstawą graniastosłupa prostego jest równoległobok o bokach a i b i kącie ostrym α. Kwadrat krawędzi bocznej graniastosłupa równa się różnicy kwadratów przekątnych podstawy. Obliczyć objętość i pole powierzchni bocznej graniastosłupa. Zad.6. W prawidłowym czworokątnym graniastosłupie bok podstawy jest równy a, a kąt między przekątną a ścianą boczną równa się α. Wyznaczyć objętość graniastosłupa. Zad.7. Przez przekątną podstawy i przekątne dwóch sąsiednich ścian bocznych prostopadłościanu poprowadzono płaszczyznę nachyloną do płaszczyzny podstawy pod kątem α takim, że tg α = ½.Obliczyę pole przekroju, jeśli wiadomo, że obwód podstawy wynosi 56, a długość średnich boków podstawy różni się o 4. Zad.8 Sześcian o krawędzi długości a=3 przecięto płaszczyzną przechodzącą przez przekątną podstawy i nachyloną do płaszczyzny podstawy pod kątem α =30º. Oblicz pole otrzymanego przekroju. Rozwiąż to samo równanie w przypadku ogólnym, przyjmując, że α Є (0º,90º )

wredulus_pospolitus: ojjj ... tylko 8 zadań czemu nie dałeś od razu 30

Karo: jestem dziewczyną jak już, poza tym nie wymagam że ktoś zrobi wszystko, będę wdzięczna nawet z jednego zadania.

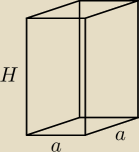
Alfa: zad.4. 8a+4H = 48 P_c = 90 a,H=? 8a+4H = 48/:4 2a + H = 12 H = 12 − 2a P_c = 2a²+4aH 2a² + 4a(12 − 2a) = 90 2a² + 48a − 8a² − 90 = 0 −6a² + 48a − 90 = 0 /:(−2) 3a² − 24a + 45 = 0 Δ = 576 − 540 = 36 √Δ = 6

	24−6
a1 =		= 3 => H1 = 12 − 6 = 6
	6

	24+6
a2 =		= 5 => H2 = 12 − 10 = 2
	6

Są więc dwa takie graniastosłupy: pierwszy o kr. podst. a = 3cm i wysokości H = 6cm drugi o kr. podst. a = 5cm i wysokości H = 2cm