rozkład różnicy zmiennych losowych hera: Niech X i Y będą niezależnymi zmiennymi losowymi o tym samym rozkładzie wykładniczym o gęstości: [tex]f(x)=\begin{cases}e^−x&\text{dla } x>0\\ 0&\text{dla } x \le 0 \end{cases}[/tex] widzę ,że forum nie ma LaTexa więc wklejam link do zadania: http://forum.zadania.info/viewtopic.php?f=39&t=61209 Wyznaczyć rozkład zmiennej losowej Z=X−Y Zadanie ze zbioru "Rachunek prawdopodobieństwa i statystyka matematyczna w zadaniach. Cz. 1, Włodzimierz Krysicki, Jerzy Bartos"

Krzysiek: P(Z≤z)=P(X−Y≤z)=∫∫_{x−y≤z,x≥0,y≥0}f(x,y)dxdy i korzystasz z niezależności zmiennych 'X' i 'Y' i wyliczasz całkę podwójną

hera: dzięki za odpowiedź, ale wiele mi to nie pomogło bo nie potrafię wyznaczyć całki, nie mogę sobie poradzić w ogóle z wyznaczeniem tego na rysunku. Czy mógłbyś mi jak krowa na rowie,krok po kroku to wytłumaczyć?

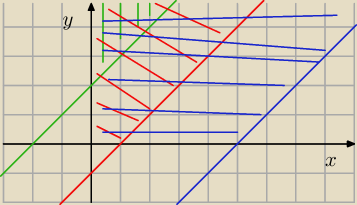
Krzysiek: wyliczasz całkę w zależności od 'z' czyli wstaw sobie kilka wartości 'z' (np. na rysunku masz: y=x−1,y=x+2,y=x−5) i zobacz jaki jest obszar całkowania.