. Piotr 10: W ostrosłupie prawidłowym czworokątnym kąt nachylenia ściany bocznej do płaszczyzny podstawy wynosi 45⁰, a odległość wierzchołka ostrosłupa od środka kuli wpisanej w ten ostrosłup równa jest 3. Oblicz pole powierzchni bocznej tego ostrosłupa. Można prosić o rysunek? Chodzi mi jak wygląda ostrosłup w którym wpisana jest kula

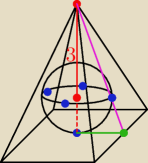
Saizou : jakoś tak

Saizou : czy pole boczne to 144√5

Piotr 10: Nie wiem, nie mam odpowiedzi, a jeszcze nie liczyłem, bo piszę wypracowanie z polaka

Saizou : jak by co to niebieskie kropki są styczne do ścian i podstawy ostrosłupa

Piotr 10: Spoko, już kończę pisać i zaraz spróbuje to zrobić

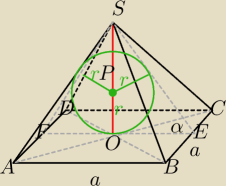
Mila: Koło wielkie kuli jest styczne (m.in.) do boków ΔFES, stąd obliczysz r. |PS|=3 ΔFES−Δprostokątny, α=45^o

Piotr 10: Jak mam wyliczyć ten promień? Bo mając promień policzę sobie wysokość ostrosłupa, potem wysokość ściany bocznej, a następnie krawędź podstawy

Saizou : jaką miarę ma kąt PSE

Piotr 10:

	3√2
Czy r=		?
	2

Piotr 10: ?

Piotr 10: ?

Mila: Tak, SP jest przekątną kwadratu o boku r.

Piotr 10:

	6+3√2
Czyli H−r=3 , H=3+r =
	2

H − wysokość ostrosłupa h − wysokość ściany bocznej

	H
cos450=
	h

	6+3√2
h=
	√2

a − długość krawędzi podstawy a=2*H=6+3√2

	6+3√2
Pb=2*a*h=2*(6+3√2)*(		)=
	√2

Dobrze ?

Saizou : a uprość to jeszcze

Piotr 10: Ale jest ok ?

Piotr 10: chyba źle mam, bo nie zgadza się z Twoim wynikiem

Saizou : mój wynik jest zły a prawidłowy to chyba 54√2+72, jeśli tym razem się nie pomyliłem xd

Piotr 10: Właśnie mam taki sam, ok dzięki wielkie

Saizou : proszę, ale to Mila zasługuje na podziękowanie

Piotr 10: Dzięki Mila też

Mila:

	6+3√2
H=
	2

a=2H a=(6+3√2) dlaczego? h_b=SE=H√2

	1		1
PΔBCS=		a*H=		*2H*H=H2
	2		2

	6+3√2
Pb=4H2=4*(		)2=(36+36√2+18)=
	2

=(54+36√2)=18(3+2√2)

Mila: Jeszcze raz sprawdzajcie Panowie.

Saizou : 3=r√2

	3√2
r=
	2

	1		3√2		6+3√2
H=		a=3+		=
	2		2		2

a=6+3√2

	6+3√2		6√2+6
h=H√2=		*√2=		=3√2+3
	2		2

	1		1
Pb=4*		ah=4*		(6+3√2)(3√2+3)=2(18√2+18+18+9√2)=2(27√2+36)=72+54√2
	2		2