Trygonometria pomocy!
MissMetja: Oblicz miarę kąta ostrego α wiedząc że:
a) tg(α+40stopni) = 1
b)1tg(α+15stopni) = √3
sin(α+40stopni) = 12 α<70 stopni
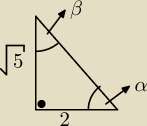
Dany jest trójkąt prostokątny o przyprostokątnych długości √5 i 2. Oblicz wartość wyrażenia
sin α−cos αsin α+cos α. Rozpatrz dwa przypadki.
Oblicz wartości pozostałych funkcji trygonometrycznych kąta ostrego α, wiedząc że:
a) 1tg α = 2
b) cos α = 23
11 lut 20:33
wredulus_pospolitus:
a) tg (jakiego kąta) = 1
| | 1 | | 1 | | √3 | |
b) |
| = √3 <=> |
| = tg(coś tam) .... tg (jakiego kąta) = |
| |
| | tg(coś tam) | | √3 | | 3 | |
11 lut 20:36
MissMetja: Nie rozumiem? Podałam wszystko jak było w zadaniu.
11 lut 20:40
wredulus_pospolitus:
ja Ciebie rozumiem ... a ja Ci podpowiadam jak masz rozwiązać to zadanie ... a jeżeli Ty
czekasz na gotowca ... to pomyliłaś miejsca −−− tutaj gotowca nie dostaniesz, bo to Ci w
niczym nie pomoże
11 lut 20:41
MissMetja: Ja po prostu nie rozumiem, co miało mi w tych "podpowiedziach" pomóc...
11 lut 20:42
MissMetja: Bo jak na tą chwilę, w podpunkcie a) mogłabym wpisać tam cokolwiek.
11 lut 20:46
wredulus_pospolitus:
pytanie:
czy znasz TABELKĘ
z wartościami sinusów,cosinusów,itd. PODSTAWOWYCH kątów
11 lut 20:48
agulka: a) tg(α+400)=tg450
11 lut 20:48
MissMetja: Agulka, dlaczego 45 ?
11 lut 20:49
agulka: tg450=1
11 lut 20:53
MissMetja: agulka, dzięki, zrozumiałam
W sumie teraz zrozumiałam też podpowiedź Wredulusa. Ale czy tak
trzeba to zrobić zadanie?
Bo b) będzie równało się 30 stopni
11 lut 20:55
MissMetja: A reszta zadań?
11 lut 20:58
MissMetja: Zaczęłam robić zadanie drugie.
Czy ktoś może jest sprawdzić?
22+√52=z2
4+5=z2
z2=9
z=3
sin α = 23
cos α = √53
Rozwiązanie : 23 − √53 / 23 + √53 = skracamy 23, zostaje −
√53 / √53 = −1
11 lut 21:11
agulka:
z=3 ok
| sinα−cosα | | | | √5−2 | | 3 | |
| = |
| = |
| * |
| = |
| sinα+cosα | | | | 3 | | √5+2 | |
11 lut 21:26
agulka: | | 2 | | √5 | |
Drugi przypadek to: sinβ= |
| , cosβ= |
| i podstawiasz do wzoru jak wyżej |
| | 3 | | 3 | |
11 lut 21:28