Planimetria
Patusia:
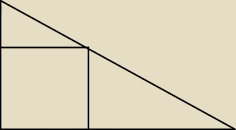
Oblicz pole kwadratu wpisanego w trójkąt prostokątny o przyprostokątnych 6 i 8,
którego dwa boki zawierają się w przyprostokątnych trójkąta.
bok kwadratu: a
przyprostokątne : x i y
przeciwprostokątna: z
x
2 +y
2 = z
2
6
2+8
2=z
2
36+64=z
2
z
2= 100
z= 10
(6−a)
2 +(8−a)
2 = 10
2
36− 12a +a
2 + 64 −16a +a
2=100
2a
2 −28a=0/:2
a
2−14=0
i dalej Δ ?
dobrze
11 lut 16:50
Hajtowy: Po co Ci delta?
a
2−14=0
a
2=14
a=
√14 v a=−
√14 
11 lut 16:54
Hajtowy: nie sprawdzałem bo mi sie nie chce
11 lut 16:55
Patusia: Hahaha, no tak, faktycznie delta mi niepotrzebna
11 lut 17:25
Patusia: Dziękuję za pomoc!
11 lut 17:27
agulka: A skąd się wzięło (6−a)2+(8−a)2=102?
11 lut 17:36
Pati: W półkole o promieniu długości 8 wpisano kwadrat w ten sposób, że jeden z boków kwadratu
zawiera
się w średnicy, a dwa wierzchołki należą do półokręgu. Oblicz stosunek pola kwadratu do pola
półkola.
Zad.2
Półprosta poprowadzona z wierzchołka kąta prostego trójkąta prostokątnego i przechodząca przez
środek okręgu wpisanego w trójkąt dzieli przeciwprostokątną w stosunku 3:4. Oblicz pole
trójkąta,
jeśli przeciwprostokątna ma długość 20.
11 lut 17:56
Patusia: Przyprostokątne mają długości 8 i 6.
Od tych długości odjęłam bok kwadratu, czyli a
11 lut 18:04
Patusia: i podstawiłam do wzoru pitagorasa, z tego wyliczyłam a i pole kwadratu
11 lut 18:06
agulka:
Skoro to są przyprostokątne to chyba 62+82=102?
11 lut 18:08
Patusia: No tak, ale chciałam wyliczyć ile ma a
11 lut 18:12
agulka: Ale to nie jest dobrze
11 lut 18:25