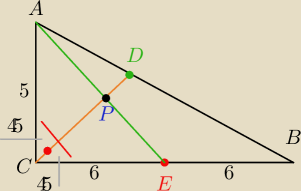
 Rysunek do zadania
Rysunek do zadania
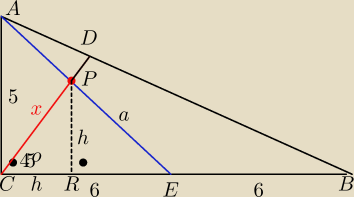 I AE I2 = 52 + 62 = 25 + 36 = 61
I AE I = √61
I CE I = 6
a = I PE I
h = I PR I = I CR I
x = I PC I
I AE I2 = 52 + 62 = 25 + 36 = 61
I AE I = √61
I CE I = 6
a = I PE I
h = I PR I = I CR I
x = I PC I
| a | h | ||
= | ⇒ 5a = h √61 ⇒ 25 a2 = 61 h2 | ||
| √61 | 5 |
| − 300 + 360 | 60 | 30 | ||||
h = | = | = | ||||
| 22 | 22 | 11 |
| 30 | ||
x = h √2 = | √2 ≈ 3,86 | |
| 11 |
| 30 | ||
Odp. | √2 cm | |
| 11 |

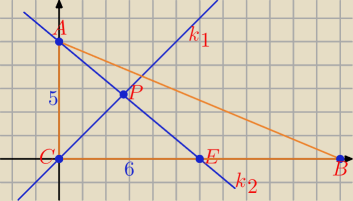 albo korzystając z narzędzi geometrii analitycznej:
albo korzystając z narzędzi geometrii analitycznej:
| 5 | ||
k1: y = x, k2: y = − | x + 5 | |
| 6 |
| 5 | 30 | 30 | ||||
P = k1∩k2 ⇒ x = − | x + 5 ⇒ x = | i y = | ||||
| 6 | 11 | 11 |
| 30 | ||
|CP| = √(30/11)2 + (30/11)2 = | √2 | |
| 11 |
 Mimo, że zadanie jest sprzed kilku godzin i jest już rozwiązane, to wracam do niego, ponieważ
chcę pokazać bardzo proste rozwiązanie.
Mimo, że zadanie jest sprzed kilku godzin i jest już rozwiązane, to wracam do niego, ponieważ
chcę pokazać bardzo proste rozwiązanie.
| 5 | x | 30 | ||||
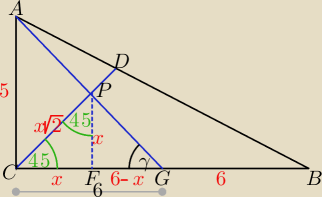
Trójkąty ACG i PFG są podobne, stąd | = | ⇒ 30 − 5x = 6x ⇒ x = | ||||
| 6 | 6 − x | 11 |
| 30 | ||
|CP| = x√2 = | √2 | |
| 11 |
