Krawędź podstawy prawidłowego ostrosłupa czworokątnego ma długość 10 cm.
Yeager: Krawędź podstawy prawidłowego ostrosłupa czworokątnego ma długość 10 cm. kąt między sąsiednimi
ścianami bocznymi ma miare 120 stopni. Oblicz pole powierzchni bocznej ostrosłupa/
Proszę bardzo ładnie o pomoc
10 lut 23:01
Uczę się:
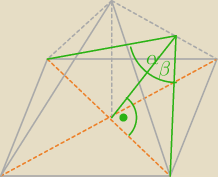
α=120
0
10 lut 23:13
Yeager: niestety dalej nie za bardzo wiem co mam z tym zrobić dalej :<
10 lut 23:21
Yeager: pomoze ktos prosze?
11 lut 00:29
dero2005:
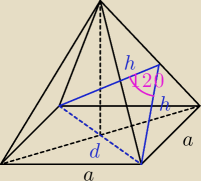
a = 10
d = a
√2 = 10
√2
d
2 = 2h
2 − 2h
2cos120
o
(10
√2)
2 = 2h
2(1 +0,5)
200 = 2h
2*1,5
| | 10 | |
Pb = 2*a*h = 2*10* |
| √6 = |
| | 3 | |
11 lut 07:14
agulka:
Pb=2*a*h? A nie Pb=2*l*h, gdzie l to krawędź ostrosłupa?
11 lut 10:55
Uczę się: nie
Pole boczne ostrosłupa prawidłowego czworokątnego tworzą cztery trójkąty równoramienne. Czyli
po skróceniu:
Pb=2*a*h
11 lut 14:43
J: Ale "a "jest krawędzią podstawy, a "h" nie jest wysokością trójkata równoramiennego ( ściany)
11 lut 14:50
Janek191:
@Dero2005
Jaką długość ma krawędź boczna ostrosłupa ?
11 lut 14:54
agulka:
@Uczę się ja wiem co tworzy pole boczne ostrosłupa, ale w tym przypadku h nie jest wysokością
opuszczoną na bok a tylko na krawędź l
11 lut 15:17
J: Dokładnie tak
11 lut 15:19
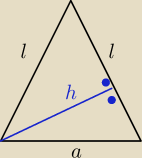
dero2005:
h
s wysokość ściany na podstawę a
l − krawędź boczna
| ⎧ | hs *a = h*l | |
| ⎩ | l2=hs2+(a2)2 |
|
12 lut 07:56