Marcin: Wyznacz najmniejszą i największą wartość funkcji f(x,y)=4x+y w obszarze wyznaczonym przez układ {−x+3y≤12 {3x+y≤24 {x≥0 {y≥0 Rysuje sobie wszystko pięknie ładnie, później rysuje prostą 4x+y=f(x,y). Tylko mam mały problem, bo u mnie ta funkcja ma tylko jeden punkt wspólny z tym obszarem i niby wartość min=max, ale takiej odpowiedzi niestety nie ma. Podpowiedzi? wartość min i max u mnie =0.

wredulus_pospolitus: ojjj ... po pierwsze ... funkcja f(x,y) jest to funkcja rysowana w R³ (przestrzeni) ... natomiast zbiór narysowany masz na płaszczyźnie (R²)

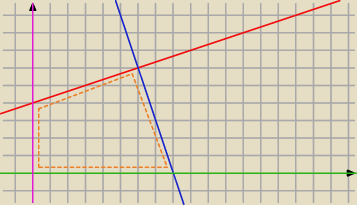
wredulus_pospolitus: taki obszar ... zauważ że f(x,y) = 4x+y będzie miało największą wartość dla jak największych zarówno 'x' jak i 'y' .. jednak o wiele bardziej istotny jest 'x' niż 'y' ... stąd wiemy, że maksimum będzie dla par (x,y) leżących na niebieskiej prostej minimum to faktycznie będzie punkt (0,0)

Saizou : Marcin skąd ty bierzesz te zadania

Marcin: No ok, a da się to po prostu obliczyć? Nie rysując, bo tego w materiale nie mam..

Marcin: Saizou to jest zadanie mojej siostry z drugiej klasy technikum (nowa matura itd)

wredulus_pospolitus: rysowania wykresów nie masz

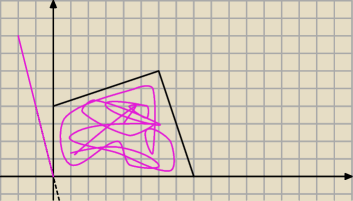
Marcin: Czyli ta różowa prosta to nie jest moja funkcja?

wredulus_pospolitus: nieeee

zawodus: Funkcji dwóch zmiennych nie ma w liceum

wredulus_pospolitus: f(x,y) = 4x+y −−−−−− z = 4x+y <−−− prosta w przestrzeni

Marcin: Mam. Wykres narysowałem bez mniejszy problemów, mam po prostu problem z odczytaniem min i max, a Ty mi jeszcze piszesz o jakiejś funkcji w przestrzeni..

Marcin: Moja siostra to ma. Druga klasa technikum

wredulus_pospolitus: Marcin ... bo to nie myśl co to za funkcja myśl kiedy wyrażenie (4x+y) przyjmuje wartość najmniejszą ... a kiedy największą

zawodus: To nie znaczy, że takie rzeczy się uczy. Nowa podstawa nie wprowadza funkcji wielu zmiennych... Ciekaw jestem jak tłumacza szukania tych ekstremów.... totalna porażka...

wredulus_pospolitus: najmniejsza gdy x=0 i y=0 ... to chyba jasne i nie trzeba tego tłumaczyć największa ... 'gdzieś na niebieskiej linii' −−− rozumiesz dlaczego akurat dla punktów z tego miejsca

Marcin: Zawodus no chyba jednak wprowadza skoro moja siostra ma to w szkole.. wredulus przykro mi, ale nie rozumiem dlaczego 'gdzieś na niebieskiej lini' Przecież swój obraz mam wyznaczony i nie wiem jak max może być gdzieś indziej

Marcin: obszar, a nie obraz

zawodus: To, że autorzy książek coś wymyślają to nie znaczy, że jest to w podstawie programowej

wredulus_pospolitus: a więc tak ... masz zmaksymalizować wyrażenie (4x+y) czyli im większe 'x' i 'y' tym lepiej stąd na pewno maksimum będzie dla jakiej pary leżącej na linii niebieskiej lub czerwonej (chodzi mi tylko o te części tych prostych ... które należą do wyznaczonego zbioru )

Marcin: Nie będę się sprzeczać, może masz rację.

Marcin: W odpowiedzi jest, że maks to 32 I ja go nie widzę w tym obszarze, ale to pewnie dlatego, że to nie zwykła funkcja

wredulus_pospolitus: maksymalna wartość ... a my jesteś na etapie dla jakich 'x' i 'y' będzie ta maksymalna wartość (dopiero później ją wyliczymy)

Marcin: Wiesz.. pierwszy raz się z czymś takim spotykam, także wybacz moją niekompetencje

Marcin: Ale.. może się myle. Dla x=6, a y=8?

zawodus: nie tylko dla tego punktu

Marcin: Albo może tam gdzie się przecina 'czerwona' z 'niebieska', czyli (8,6)? Wybaczcie te strzały..

Bogdan: To jest zagadnienie rozpatrywane przez Programowanie liniowe. Funkcja z = 4x + y to funkcja celu. Funkcja osiąga w punkcie optymalnym (8, 0) wartość f(8, 0) =4*8+0 = 32. Tu jest podobny przykład http://www.maslowski.pl/index.php?id=lekcja3

Marcin: Dziękuję bardzo Panie Bogdanie

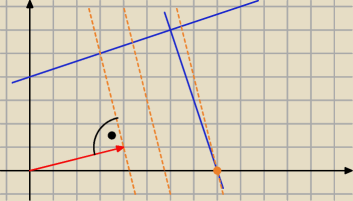
Bogdan: ten rysunek wyjaśnia rozwiązanie