Zadania optymalizacyjne Fernani: Zadanie optymalizacyjne Trójkąt prostokątny obraca się wokół osi obrotu którą jest przeciwprostokątna. Znaleźć takie boki trójkąta, że V tej figury (dwóch złożonych stożków), będzie największa. Obwód trójkąta to 2. Proszę o pomoc

Fernani: doszedłem do tego, że (przyprostokątne x,y przeciw prostokątna z) = V = 1/3πr² z i układ równań xy/2 = zr/2 x² + y² = z² x+y+z =2 ale co dalej ,

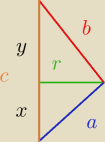Ada: Więc V=V₁+V₂

	1
V1=		πr2x
	3

	1
V2=		πr2y
	3

	1		1
V=		πr2(x+y)=		r2πc
	3		3

	1
P=		cr−> pole trójkąta
	2

1		1		ab
	ab=		cr ⇒ r=
2		2		c

a+b+c=2 (a+b)²=(2−c)² a²+b²+2ab=4−4c+c² c²+2ab=4−4c+c² ab=2−2c

	1−c
r=2
	c

	1		4(1−c)2		1		4(1−c)2
V(c)=		π		*c=		π
	3		c2		3		c