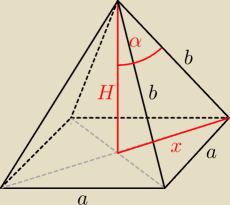
Ostrosłup Pole powierzchni i Objętość Radek: Ostrosłup Pole powierzchni i Objętość Pole powierzchni bocznej P_b=64 cm², kąt między wysokością a ściną boczną α=30 x=^a√2₂ Jeśli suma pół boczny to 64 cm² To pole boczne jednej ściany bocznej to 16 cm² Wzór na pole boczne to P_b=¹₂ah Jak dalej coś obliczyć Dziękuje za pomoc

Marcin: Jeżeli w podstawie masz kwadrat, a ostrosłup jest prawidłowy, to faktycznie Pb będzie się składać z 4 takich samych trójkątów.

Radek: Ściany boczne to cztery trójkąty równoboczne przystające

Marcin: Skoro to cztery trójkąty równoboczne, to wzór na poje jednego to będzie

a2√3
	=16
4

Radek: Niee równoboczne nie mogą być, muszą być równoramienne

Marcin: Sam tak napisałeś

Radek: no to poprawiam się że są to równoramienne

Marcin: Tak w ogóle, to masz źle zaznaczony kąt w tym ostrosłupie. Ty zaznaczyłeś kąt między wysokością, a krawędzią boczną, a nie ścianą .

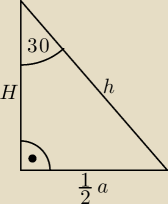
Radek: Jeśli 16=¹₂ah to h=³²_a?

Radek: I czy te pole powierzchni bocznej to jest pole sumy czy jednej ściany?

Marcin: To pole to jest pole jednej ściany Licz dalej

Radek: to wtedy h=¹²⁸_a sin30=^1₂a_h a=8√2 Dobrze ?

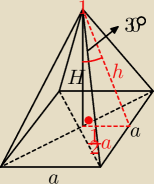
agulka: P_b=64

	1
Pb=4*		*a*h
	2

64=2ah

	1   a 2
sin300=
	h

1		a
	=
2		2h

a=h 64=2a²⇒a=4√2 h=4√2

	1
H2=h2−(		a)2
	2

H²=32−8 H²=24 H=2√6 P_p=a²=32

	1
V=		*Pp*H
	3

V=... P_c=P_p+P_b P_c=...