równania

równania Radek: Rozwiąż równanie w przedziale <0,2π> 4+sinxcosx−5sin²x=4cosx=0 sinxcosx−sin²x−9 sinx(cosx−sinx)=0 sinx=0 cosx=sinx

	π
x=0 lub x=π x=2π x=
	4

10 lut 20:03

wredulus_pospolitus: yyy ... jak z 4cos²x+4cosx zrobiłeś '−9'

10 lut 20:04

Radek: klawisz obok nacisnąłem przez pomyłkę.

10 lut 20:11

wredulus_pospolitus: no to nadal jak z 4cos²x + 4cosx wyszło Ci '0'

10 lut 20:13

Radek: Jeszcze raz napisze wyjściowe 4+sinxcosx−5sin²x=4cos²x Przepraszam za zamieszanie.

10 lut 20:17

wredulus_pospolitus: aaa widzisz ... całkowicie inaczej to teraz wygląda emotka

ok,ok,ok,ok ... wygląda dobrze

10 lut 20:19

Radek: Mogę Cię jeszcze prosić o pomoc ?

10 lut 20:22

wredulus_pospolitus: prosić zawsze można emotka

10 lut 20:24

Radek: Mam takie równanie

cos³α+sin²αcosα
	=2
cos²α

Nie chcę żeby ktoś pisał i kazał dokończyć Czy tutaj muszę zrobić założenie cos²α≠0 ?

10 lut 20:30

wredulus_pospolitus: oczywiście ... bez tego założenia ten ułamek jest pozbawiony sensu

10 lut 20:31

Radek:

	π
x≠{		+kπ k∊C}
	2

10 lut 20:33

wredulus_pospolitus: yhy

10 lut 20:35

Radek:

	π		5π
x=		+2kπ lub x=		+2kπ
	3		3

10 lut 20:39

wredulus_pospolitus:

	1
cosa =		... yyy ... ok
	2

10 lut 20:43

Radek: A mam jeszcze podobne zadanie do tego więc od razu wstawię Wyznacz miarę kąta ostrego α , dla którego to wyrażenie ma wartość 2 I w tym wypadku też trzeba ustalać dziedzinę ? x=60⁰ (wyrażenie takie jak poprzednie)

10 lut 20:44

Mila: Dobrze.

10 lut 20:45

Mila: Dziedzinę też.

10 lut 20:46

Radek: Dziękuję.

10 lut 20:46

Radek: Wyznacz największe ujemne rozwiązanie równania sin(−2x)=sinx −2sinxcox−sinx=0 2sinxcosx+sinx=0 sinx(2cosx+1)=0

	1
sinx=0 lub cosx=−
	2

	5π		5π
x=kπ lub x=		+2kπ lub x=−		+2kπ
	6		6

10 lut 21:05

wredulus_pospolitus: no i jakie jest największe ujemne rozwiązanie

10 lut 21:07

Radek:

	5π
x=−		+2kπ
	6

	2π
w odp x=−		+2kπ ?
	3

10 lut 21:08

wredulus_pospolitus:

	2
jasne że		π
	3

	1
dla jakiego kąta cosx = +		no na pewno nie ma to nic związanego z 30^o
	2

10 lut 21:10

Mila:

	−1
cosx=		źle rozwiązałeś.
	2

10 lut 21:11

Radek:

	1
Przecież dobrze rozwiązałem cosx=−
	2

10 lut 21:12

wredulus_pospolitus: niii ... ni ho ho ... te kąty nie dla takiej wartości cosinusa

10 lut 21:13

Radek:

	1
A jeśli ten cosx=−		miałby być w przedziale <0,2π> to jest prawidłowe rozwiązanie ?
	2

10 lut 21:14

wredulus_pospolitus: Radek ... nie

5
	π = 180 − 30 = 150^o
6

	√3
cos (150^o) = −cos(180−150) = −cos30^o = −
	2

10 lut 21:16

Radek: Ale czy jeśli miałbym takie równanie w przedziale <0,2π>

	1
to czy rozwiązanie cosx=−		jest poprawne o to pytam ?
	2

10 lut 21:18

wredulus_pospolitus: tak ... do tego momentu masz wszystko dobrze ... po prostu źle wyznaczyłeś x z tego

	1
cosx=−
	2

10 lut 21:26

Radek: Ale nawet jak inaczej rozwiążę to nie wychodzi tak jak w książce

10 lut 21:33

wredulus_pospolitus: wyjdzie dobrze ... jak dobrze rozwiążesz

10 lut 21:43

Radek:

	π		π
x=−		lub x=
	3		3

10 lut 22:05

wredulus_pospolitus:

	1
radek ... te kąty są dla cosx = +
	2

10 lut 22:07

Radek:

	π
π−
	3

	2π		2π
x=		lub x=−
	3		3

10 lut 22:08

wredulus_pospolitus: ooo ... i teraz masz dobrze

10 lut 22:09

Radek: w końcu dzięki

10 lut 22:09

Mila:

Oj, Radek.

	1
cosx=−
	2

	π		π
x=		+π+2kπ lub x= −		+π+2kπ
	3		3

	4		2π
x=		π+2kπ lub x=		+2kπ obydwa dodatnie
	3		3

	2π
x=−		najwieksze ujemne rozwiązanie
	3

10 lut 22:15

Radek: Ja wiem jak rozwiązać w przedziale ale gubię się z normalnym rozwiązaniem

10 lut 22:19

zawodus: Ale to z normalnego rozwiązania wyznacza się te w przedziale...

10 lut 22:20

Radek: podaj jakieś równanie,

10 lut 22:22

zawodus: Ja?

10 lut 22:31

Radek: Tak.

10 lut 22:32

Radek: Maturalne...

10 lut 22:33

zawodus: Spoko myślę

rozwiąż równanie

	1
sin⁴x−cos⁴x=		w przedziale <0,2π>
	2

10 lut 22:42

zawodus: 2. rozwiąż równanie: 2cos2x−4cosx+3−0 w przedziale <−2π, 2π>

10 lut 22:45

Radek:

	1
sin⁴x−cos⁴x=		/2
	2

2sin⁴x−2cos⁴x=1 2sin⁴x−2(1−sin²x)²−1=0 2sin⁴x−2(1−2sin²x+sin⁴x)−1=0 2sin⁴x−2+4sin²x−2sin⁴x−1=0 4sin²x−3=0

	3
sin²=
	4

	√3		√3
sinx=		lub x=−
	2		2

	π
x=
	3

	π		2π
x=π−		=
	3		3

	π
x=−		+2π
	3

	5π		4π
x=		lub x=
	3		3

10 lut 22:54

Radek: 2cos2x−4cosx+3=0 w przedziale <−2π, 2π> 2(cos²x−sin²x)−4cosx+3=0 2cos²x−2sin²x−4cosx+3=0 2cos²x−2(1−cos²x)−4cosx+3=0 2cos²x−2+2cos²x−4cosx+3=0 4cos²x−4cosx+1=0 (2cosx−1)²=0 2cosx=1

	1
cosx=
	2

	π		π
x=		lub x=−
	3		3

10 lut 23:01

Radek: Z takimi to sobie radzę ale proste równania proszę takie bez przedziałów.

10 lut 23:01

Piotr 10: jeśli chodzi Ci o zadanie ostatnie to nie podałeś wszystkich rozwiązań, masz przedział <−2π;2π>, popatrz na wykresik

10 lut 23:03

Radek:

	7π
x=
	6

	7π
x=−
	6

10 lut 23:07

zawodus: No właśnie niby takie proste

10 lut 23:07

zawodus: Niestety, ale źle.

10 lut 23:08

Radek: które ?

10 lut 23:08

zawodus: Te dwa co dopisałeś

10 lut 23:10

Radek: to jakie powinny być prawidłowe ?

10 lut 23:11

zawodus: Proste równania

	1
1. sinx=
	2

	√3
2. tgx=
	2

	1
3. sinx=−
	2

4. sinx=−{√3}{2}

	1
5. cosx=−
	2

	√2
6. cosx=−
	2

Proste nierówności:

	1
7. sinx>
	2

8. cosx≤1 9. tgx>1

	1
10. sinx<−
	2

	1		√3
11.		<sinx<
	2		2

10 lut 23:14

zawodus:

	5		5
−		π,		π
	3		3

Licz równania i nierówności

10 lut 23:14

Marcin: Radek faktycznie miałeś źle. Popatrz na cosinusoide emotka

10 lut 23:17

Radek:

	1
sinx=
	2

	π		π
x=		+2kπ lub x=π−		+2kπ
	6		6

	5π
x=		+2kπ
	6

10 lut 23:19

Marcin: zawadous..

	√2		π
czyli np cosx=−		= −		?
	2		4

10 lut 23:20

Radek:

	√3
tgx=
	3

	π
x=		+kπ
	6

10 lut 23:20

Radek:

	1
sinx=−
	2

	π		π
x=−		+2kπ lub x=π+
	6		6

	7π
x=		+2kπ
	6

10 lut 23:21

Radek:

	√3
sinx=−
	2

	π		π
x=−		+2kπ lub x=π+		+2kπ
	3		3

	4π
x=		+2kπ
	3

10 lut 23:23

Radek:

	√2
cosx=−
	2

	π
x=π−
	4

	3π		3π
x=		+2kπ lub x=−		+2kπ
	4		4

10 lut 23:24

zawodus: Marcin raczej to nie jest tyle

10 lut 23:24

Marcin: ok, ok. Już sam do tego doszedłem

10 lut 23:26

zawodus: Na razie ok

10 lut 23:30

Radek: nierówności to sobie na razie daruję i tak nie ma ich na maturze R ?

10 lut 23:31

zawodus: Są nierówności. Równań też teoretycznie trudniejszych niż te co podałem być nie może

10 lut 23:34

Radek:

	π		5π
7 x∊(		,		)
	6		6

10 lut 23:36

Mariush: Radek,o jakim wierszyku mowila ci p.Mila o wzorach redukcyjnych,ta mi sie wydaje)pytala,czy wiesz go...

10 lut 23:37

Marcin: Ja nierówności prawie nie ogarniam, ale te które podałeś to zrobiłem bez jakiegoś problemu emotka

	√2
Muszę się jeszcze nauczyć zaznaczać na cosinusoidzie np cosx=		i będę happy
	2

10 lut 23:38

Radek: Wiem o wierszyku.

10 lut 23:38

Mariush: powiedz prosze emotka

10 lut 23:40

Radek: w pierwszej wszystkie są dodatnie, w drugiej tylko sinus,w trzeciej tangens i cotanges,a w czwartej cosinus

10 lut 23:41

zawodus: Jaki wierszyk?

twórczość ludowa?

10 lut 23:42

zawodus: A ten to znam

10 lut 23:42

Mariush: dziekuje) czemu w rownaniach z sinusami masz +2πn,o ile wiem jest +πn

10 lut 23:44

Marcin: Wiecie gdzie jest jakiś poradnik jak zaznaczać cokolwiek na sinusoidach czy cosinusoidach? Jeżeli macie gdzieś coś, takiego, to bardzo prosiłbym o podzielenie się ze mną emotka

10 lut 23:44

Radek: To chyba źle wiesz...

10 lut 23:49

zawodus: Na pewno źle wie

10 lut 23:53

Radek: Mogę jeszcze prosić o wytłumaczenie 22:15

11 lut 17:15

Radek: ?

11 lut 17:56

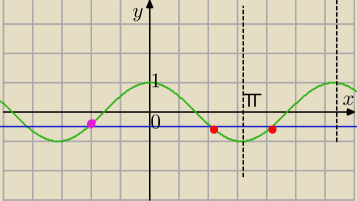
Mila: Radek w przedziale (0,2π) zaznaczyłam dwa rozwiązania równania ( czerwone punkty przecięcia )

	1
cosx=−		,
	2

W zadaniu proszą o rozwiązanie ujemne (x<0). funkcja cos x jest funkcją parzystą

	2π		2π
cos(		)=cos(−		)
	3		3

	4π		4π
cos(		)=cos(−		)
	3		3

	2π		4π
(−		)>(−		)
	3		3

największe ujemne rozwiązanie podanego równania to:

	2π
x=(−		)
	3

11 lut 18:06

Radek:

	1
Ale chodzi o rozwiązanie cosx=−
	2

	2π		2π
x=		+2kπ lub x=−		+2kπ
	3		3

11 lut 18:10

Mila:

	1
cosx=
	2

	π		π
x=		+2kπ lub x=−		+2kπ patrz wykres
	3		3

Rozwiązanie dla równania

	1
cosx=−		buduję tak:
	2

	π		π
x=		+π+2kπ lub x=−		+π+2kπ patrz wykres, albo tabelke, która na pewno
	3		3

dostałeś w szkole.

	2π		4π
Stad x=		+2kπ lub x=		+2kπ
	3		3

11 lut 18:26

Radek: Ja zawsze robiłem tak, że najpierw

	π
π−		+2kπ
	3

2π		−2π
	+2kπ a drugi z przeciwnym znakiem czyli x=		+2kπ
3		3

11 lut 18:30

Mila: Też dobrze. A jeśli poproszą o rozwiązania w przedziale (0,2π)? Poradzisz sobie?

11 lut 18:52

Radek: To muszę do ujemnego dodać 2π ?

11 lut 18:53

Mila: Tak.

11 lut 18:54

Radek: Dziękuję. Jak by Pani mogła jeszcze udzielić kilku wskazówek w nowym temacie to byłbym bardzo wdzięczny emotka

11 lut 19:01

Mila: Pisz. I czekaj .

11 lut 19:04